已知数轴上两点A、B对应的数分别为-1、3, 点P是数轴上一动点P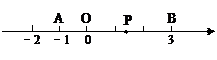
（1）(4分)若点P到点A,点B的距离相等,求点P对应的数；
（2） (6分)当点P以每分钟5个单位长度的速度从O点向右运动时,点A以每分钟3个单位长度的速度向右运动,点B以每分钟2个单位长度的速度向右运动,问几分钟时点P到点A,点B的距离相等.
已知数轴上两点A、B对应的数分别为-1、3, 点P是数轴上一动点P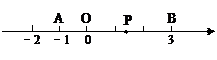
（1）(4分)若点P到点A,点B的距离相等,求点P对应的数；
（2） (6分)当点P以每分钟5个单位长度的速度从O点向右运动时,点A以每分钟3个单位长度的速度向右运动,点B以每分钟2个单位长度的速度向右运动,问几分钟时点P到点A,点B的距离相等.
.
、
在第一象限的图像，
，过
，作
轴的平行线交
，交
轴于
，若
；求双曲线
中，
． 
＞
．
．
粤公网安备 44130202000953号