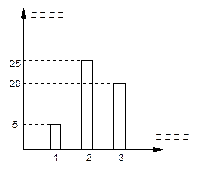西安市某中学号召学生在2010年春节期间至少参加一次社会公益活动．经统计，该校高三（1）班共50名学生参加公益活动情况如图所示．
（Ⅰ）从高三（1）班任选两名学生，求他们参加活动次数恰好相等的概率；
（Ⅱ）从高三（1）班任选两名学生，用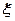
表示这两人参加活动次数之差的绝对值，求随机变量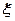的分布列及均值
．
相关试题
的离心率为
，点
是双曲线的一个顶点．
作倾斜角为30°直线
，直线
两点,求
的长．
:
，命题
: 对任何
R，都有
，命题
的取值范围．
，
，则“
，或
”是“
”的什么条件？
，且
，
，
，使得
在
上为减函数，并且在
上为增函数，若不存在，说明理由.
时，求
.
对任意
,都有
, 
且当
时，都有
.
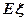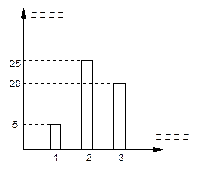
上单调递减.相关知识点
推荐套卷
西安市某中学号召学生在2010年春节期间至少参加一次社会公益活动．经统计，该校高三（1）班共50名学生参加公益活动情况如图所示．
（Ⅰ）从高三（1）班任选两名学生，求他们参加活动次数恰好相等的概率；
（Ⅱ）从高三（1）班任选两名学生，用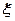表示这两人参加活动次数之差的绝对值，求随机变量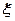的分布列及均值．
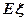粤公网安备 44130202000953号