某高等学校自愿献血的50位学生的血型分布的情况如下表：
| 血型 |
A |
B |
AB |
O |
| 人数 |
20 |
10 |
5 |
15 |
(1) 从这50位学生中随机选出2人，求这2人血型都为A型的概率；
（2）现有一位血型为A型的病人需要输血，要从血型为A，O的学生中随机选出2人准备献血，记选出A型血的人数为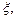
求随机变量
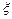的分布列及数学期
望．
、
、
≥0，且
，求证
≥
、
、
是三角形的边长，求证：
≥
、
、
是三角形的边长，求证
≥3
（a∈R）．(1)若
在[1，e]上是增函数，求a的取值范围；（2）若a=1,a≤x≤e,证明：
相关知识点
推荐套卷
某高等学校自愿献血的50位学生的血型分布的情况如下表：
| 血型 |
A |
B |
AB |
O |
| 人数 |
20 |
10 |
5 |
15 |
(1) 从这50位学生中随机选出2人，求这2人血型都为A型的概率；
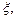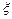（2）现有一位血型为A型的病人需要输血，要从血型为A，O的学生中随机选出2人准备献血，记选出A型血的人数为求随机变量的分布列及数学期望．
粤公网安备 44130202000953号