(本小题满分12分)
甲、乙两运动员进行射击训练,已知他们击中的环数都稳定在7,8,9,10环,且每次射击成绩互不影响.射击环数的频率分布条形图如下: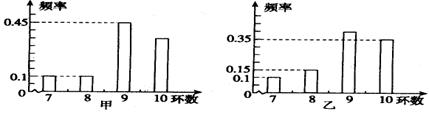
若将频率视为概率,回答下列问题:
(I)求甲运动员在3次射击中至少有1次击中9环以上(含9环)的概率;
(II)若甲、乙两运动员各自射击1次, 表示这2次射击中击中9环以上(含9环)的次数,求
表示这2次射击中击中9环以上(含9环)的次数,求 的分布列及
的分布列及 .
.
相关知识点
推荐套卷
(本小题满分12分)
甲、乙两运动员进行射击训练,已知他们击中的环数都稳定在7,8,9,10环,且每次射击成绩互不影响.射击环数的频率分布条形图如下:
若将频率视为概率,回答下列问题:
(I)求甲运动员在3次射击中至少有1次击中9环以上(含9环)的概率;
(II)若甲、乙两运动员各自射击1次, 表示这2次射击中击中9环以上(含9环)的次数,求
表示这2次射击中击中9环以上(含9环)的次数,求 的分布列及
的分布列及 .
.