甲,乙两人进行射击比赛,每人射击6次,他们命中的环数如下表:
| 甲 |
5 |
8 |
7 |
9 |
10 |
6 |
| 乙 |
6 |
7 |
4 |
10 |
9 |
9 |
(1)根据上表中的数据,判断甲,乙两人谁发挥较稳定;
(2)把甲6次射击命中的环数看成一个总体,用简单随机抽样方法从中抽取两次命中的环数组成一个样本,求该样本平均数与总体平均数之差的绝对值不超过0.5的概率.
相关知识点
推荐套卷
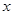 轴的正半轴为极轴建坐标系,已知曲线
轴的正半轴为极轴建坐标系,已知曲线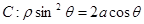
 ,已知过点
,已知过点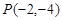 的直线
的直线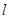 的参数方程为
的参数方程为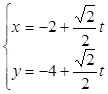 (
(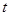 为参数),直线
为参数),直线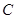 分别交于
分别交于 两点。
两点。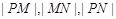 成等比数列,求
成等比数列,求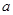 的值.
的值.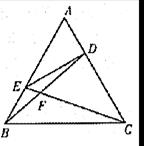
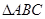 中,点
中,点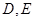 分别在边
分别在边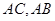 上,且
上,且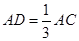 ,
,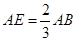 ,
,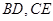 相交于点
相交于点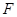
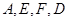 四点共圆;
四点共圆;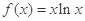 (
(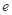 为无理数,
为无理数,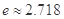 )
)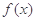 在点
在点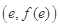 处的切线方程;
处的切线方程;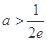 ,求函数
,求函数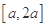 上的最小值;
上的最小值;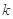 为正整数,且
为正整数,且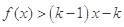 对任意
对任意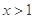 恒成立,求
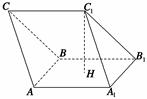
恒成立,求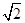 ,C1H⊥平面AA1B1B,且C1H=
,C1H⊥平面AA1B1B,且C1H=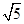 .
.
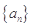 中,
中, ,前项和
,前项和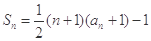 .
.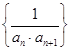 的前项和为
的前项和为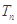 ,是否存在实数
,是否存在实数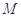 ,使得
,使得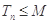 对一切正整数都成立?若存在,求出
对一切正整数都成立?若存在,求出 粤公网安备 44130202000953号
粤公网安备 44130202000953号