(本题满分14分)口袋中有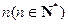
个白球和3个红球．依次从口袋中任取一球，如果取到红球，那么继续取球，且取出的红球不放回；如果取到白球，就停止取球．记取球的次数为X．若
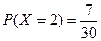，求：
（1）n的值；
（2）X的概率分布与数学期望．
相关试题
在区间
上的最值。(要列表求)
在
处取得极值,并且
在点( 1 , 0 ) 处相切, 求a , b , c的值。
是定义域为R的奇函数；
，试求不等式
的解集；
上的最小值为－2，
a－
的最大值为1时a的值．
的最小正周期为
，
．
，
；
的单调递减区间；
上的图象．
相关知识点
推荐套卷
(本题满分14分)口袋中有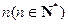个白球和3个红球．依次从口袋中任取一球，如果取到红球，那么继续取球，且取出的红球不放回；如果取到白球，就停止取球．记取球的次数为X．若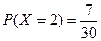，求：
（1）n的值；
（2）X的概率分布与数学期望．
粤公网安备 44130202000953号