2010年4月14日清晨我国青海省玉树县发生里氏7.1级强震。国家抗 震救灾指挥部迅速成立并调拨一批救灾物资从距离玉树县400千米的某地A运往玉树县,这批救灾物资随17辆车以
震救灾指挥部迅速成立并调拨一批救灾物资从距离玉树县400千米的某地A运往玉树县,这批救灾物资随17辆车以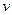 千米/小时的速度匀速直达灾区,为了安全起见,每两辆车之间的间距不得小于
千米/小时的速度匀速直达灾区,为了安全起见,每两辆车之间的间距不得小于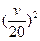 千米。设这批救灾物资全部运送到灾区(不考虑车辆的长度)所需要的时间为
千米。设这批救灾物资全部运送到灾区(不考虑车辆的长度)所需要的时间为 小时。求这批救灾物资全部运送到灾区所需要的最短时间,并指出此时车辆行驶的速度。
小时。求这批救灾物资全部运送到灾区所需要的最短时间,并指出此时车辆行驶的速度。
相关知识点
推荐套卷
2010年4月14日清晨我国青海省玉树县发生里氏7.1级强震。国家抗 震救灾指挥部迅速成立并调拨一批救灾物资从距离玉树县400千米的某地A运往玉树县,这批救灾物资随17辆车以
震救灾指挥部迅速成立并调拨一批救灾物资从距离玉树县400千米的某地A运往玉树县,这批救灾物资随17辆车以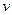 千米/小时的速度匀速直达灾区,为了安全起见,每两辆车之间的间距不得小于
千米/小时的速度匀速直达灾区,为了安全起见,每两辆车之间的间距不得小于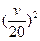 千米。设这批救灾物资全部运送到灾区(不考虑车辆的长度)所需要的时间为
千米。设这批救灾物资全部运送到灾区(不考虑车辆的长度)所需要的时间为 小时。求这批救灾物资全部运送到灾区所需要的最短时间,并指出此时车辆行驶的速度。
小时。求这批救灾物资全部运送到灾区所需要的最短时间,并指出此时车辆行驶的速度。