已知函数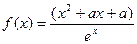 ,(
,(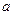 为常数,
为常数,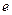 为自然对数的底).
为自然对数的底).
(1)令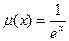 ,
,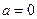 ,求
,求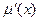 和
和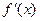 ;
;
(2)若函数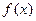 在
在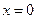 时取得极小值,试确定
时取得极小值,试确定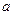 的取值范围;
的取值范围;
[理](3)在(2)的条件下,设由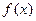 的极大值构成的函数为
的极大值构成的函数为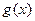 ,试判断曲线
,试判断曲线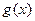 只可能与直线
只可能与直线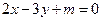 、
、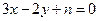 (
(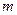 ,
,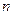 为确定的常数)中的哪一条相切,并说明理由.
为确定的常数)中的哪一条相切,并说明理由.
推荐套卷
已知函数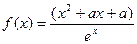 ,(
,(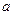 为常数,
为常数,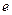 为自然对数的底).
为自然对数的底).
(1)令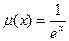 ,
,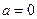 ,求
,求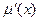 和
和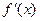 ;
;
(2)若函数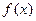 在
在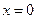 时取得极小值,试确定
时取得极小值,试确定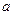 的取值范围;
的取值范围;
[理](3)在(2)的条件下,设由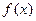 的极大值构成的函数为
的极大值构成的函数为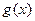 ,试判断曲线
,试判断曲线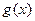 只可能与直线
只可能与直线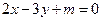 、
、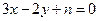 (
(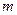 ,
,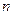 为确定的常数)中的哪一条相切,并说明理由.
为确定的常数)中的哪一条相切,并说明理由.