(本小题满分13分)某企业准备招聘一批大学生到本单位就业,但在签约前要对他们的某项专业技能进行测试。在待测试的某一个小组中有男、女生共10人(其中女生人数多于男生人数),如果从中随机选2人参加测试,其中恰为一男一女的概率为 (I)求该小组中女生的人数; (II)假设此项专业技能测试对该小组的学生而言,每个女生通过的概率均为
(I)求该小组中女生的人数; (II)假设此项专业技能测试对该小组的学生而言,每个女生通过的概率均为 ,每个男生通过的概率均为
,每个男生通过的概率均为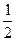 ,现对该小组中男生甲、男生乙和女生丙3个人进行测试,记这3人中通过测试的人数为随机变量
,现对该小组中男生甲、男生乙和女生丙3个人进行测试,记这3人中通过测试的人数为随机变量 ,求
,求 的分布列和数学期望。
的分布列和数学期望。
相关知识点
推荐套卷
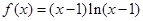 .
.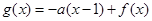 在区间
在区间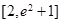 上不单调,求实数
上不单调,求实数 的取值范围;
的取值范围;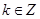 ,且
,且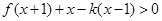 对
对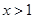 恒成立,求
恒成立,求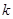 的最大值.
的最大值.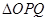 中,
中,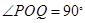 ,
,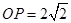 ,点
,点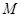 在线段
在线段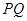 上.
上.
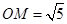 ,求
,求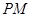 的长;
的长;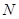 在线段
在线段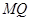 上,且
上,且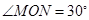 ,问:当
,问:当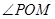 取何值时,
取何值时,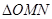 的面积最小?并求出面积的最小值.
的面积最小?并求出面积的最小值.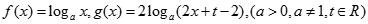 .
.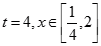 时,
时,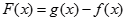 的最小值是
的最小值是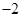 ,求
,求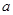 的值;
的值;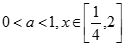 时,有
时,有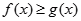 恒成立,求实数
恒成立,求实数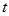 的取值范围.
的取值范围.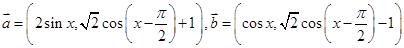 ,设
,设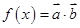 .
.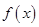 的最小正周期和单调增区间;
的最小正周期和单调增区间;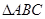 中,
中,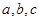 分别为
分别为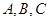 的对边,且
的对边,且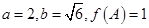 ,求边
,求边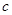 .
.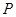 :函数
:函数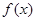 为定义在
为定义在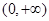 上的单调递减函数,实数
上的单调递减函数,实数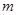 满足不等式
满足不等式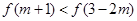 .命题
.命题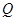 :当
:当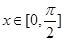 时,方程
时,方程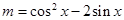 有解.求使“
有解.求使“ 粤公网安备 44130202000953号
粤公网安备 44130202000953号