袋子里有大小相同的3个红球和4个黑球,今从袋子里随机取球.
(Ⅰ)若有放回地摸出4个球,求取出的红球数不小于黑球数的概率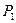 ;
;
(Ⅱ)若无放回地摸出4个球,
①求取出的红球数ξ的概率分布列和数学期望;
②求取出的红球数不小于黑球数的概率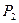 ,并比较
,并比较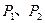 的大小.
的大小.
相关知识点
推荐套卷
袋子里有大小相同的3个红球和4个黑球,今从袋子里随机取球.
(Ⅰ)若有放回地摸出4个球,求取出的红球数不小于黑球数的概率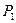 ;
;
(Ⅱ)若无放回地摸出4个球,
①求取出的红球数ξ的概率分布列和数学期望;
②求取出的红球数不小于黑球数的概率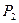 ,并比较
,并比较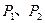 的大小.
的大小.