2007年全国统一高考理科数学试卷(北京卷)
已知 ,那么角 是()
| A. | 第一或第二象限角 | B. | 第二或第三象限角 |
| C. | 第三或第四象限角 | D. | 第一或第四象限角 |
平面 平面 的一个充分条件是( )
| A. | 存在一条直线 |
| B. | 存在一条直线 |
| C. | 存在两条平行直线 |
| D. | 存在两条异面直线 |
记者要为5名志愿者和他们帮助的2位老人拍照,要求排成一排,2位老人相邻但不排在两端,不同的排法共有()
| A. | 1440种 | B. | 960种 | C. | 720种 | D. | 480种 |
如果正数 满足 ,那么()
| A. | ,且等号成立时 的取值唯一 |
| B. | ,且等号成立时 的取值唯一 |
| C. | ,且等号成立时 的取值不唯一 |
| D. | ,且等号成立时 的取值不唯一 |
对于函数①
,②
,③
,判断如下三个命题的真假:
命题甲:
是偶函数;
命题乙:
在
上是减函数,在
上是增函数;
命题丙:
在
上是增函数.
能使命题甲、乙、丙均为真的所有函数的序号是( )
| A. | ①③ | B. | ①② | C. | ③ | D. | ② |
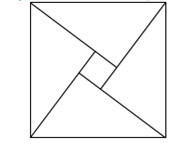
2002年在北京召开的国际数学家大会,会标是以我国古代数学家赵爽的弦图为基础设计的.弦图是由四个全等直角三角形与一个小正方形拼成的一个大正方形(如图).如果小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为
,那么
的值等于 .
数列
中,
(
是常数,
),且
成公比不为1的等比数列.
(I)求
的值;
(II)求
的通项公式.
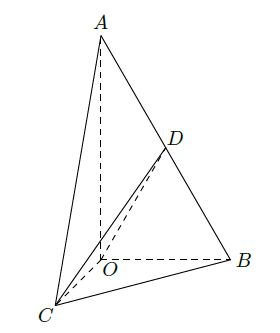
如图,在
中,
,斜边
.
可以通过
以直线
为轴旋转得到,且二面角
是直二面角.动点
的斜边
上.
(I)求证:平面
平面
;
(II)当
为
的中点时,求异面直线
与
所成角的大小;
(III)求
与平面
所成角的最大值.
矩形
的两条对角线相交于点
,
边所在直线的方程为
,点
在
边所在直线上.
(I)求
边所在直线的方程;
(II)求矩形
外接圆的方程;
(III)若动圆
过点
,且与矩形
的外接圆外切,求动圆
的圆心的轨迹方程.
某中学号召学生在今年春节期间至少参加一次社会公益活动(以下简称活动).该校合唱团共有100名学生,他们参加活动的次数统计如图所示.
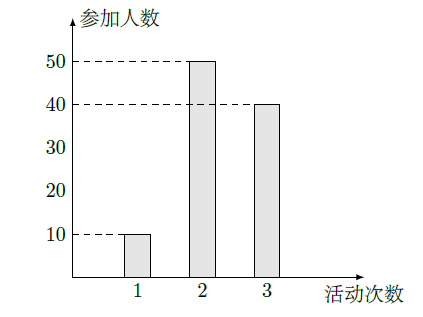
(I)求合唱团学生参加活动的人均次数;
(II)从合唱团中任意选两名学生,求他们参加活动次数恰好相等的概率.
(III)从合唱团中任选两名学生,用
表示这两人参加活动次数之差的绝对值,求随机变量
的分布列及数学期望
.
如图,有一块半椭圆形钢板,其半轴长为
,短半轴长为
,计划将此钢板切割成等腰梯形的形状,下底
是半椭圆的短轴,上底
的端点在椭圆上,记
,梯形面积为
.
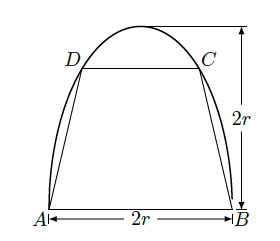
(I)求面积
以
为自变量的函数式,并写出其定义域;
(II)求面积
的最大值.

 是有序数对,集合
和
中的元素个数分别为
和
.若对于任意的
,总有
,则称集合
具有性质
.
是有序数对,集合
和
中的元素个数分别为
和
.若对于任意的
,总有
,则称集合
具有性质
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号