2009年全国统一高考理科数学试卷(安徽卷)
考察正方体6个面的中心,甲从这6个点中任意选两个点连成直线,乙也从这6个点中任意选两个点连成直线,则所得的两条直线相互平行但不重合的概率等于()

| A. | B. | C. | D. |
点
在椭圆
上,
直线
与直线
垂直,
为坐标原点,直线
的倾斜角为
,直线
的倾斜角为
.
(I)证明: 点
是椭圆
与直线
的唯一交点;
(II)证明:
构成等比数列.
来源:2009届高三数学模拟试题
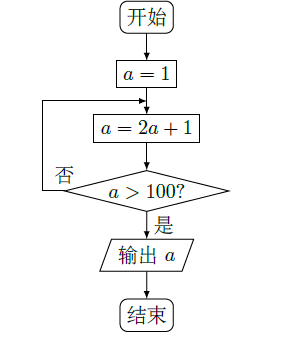
首项为正数的数列
满足
.
(Ⅰ)证明:若
为奇数,则对一切
,
都是奇数;
(Ⅱ)若对一切
,都有
,求
的取值范围。
来源:2009年高三数学推理与证明测试题(理)
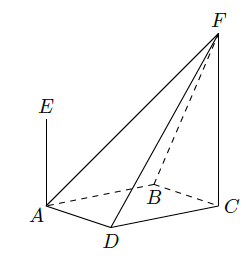
对于四面体
,下列命题正确的是(写出所有正确命题的编号).
①相对棱
与
所在的直线异面;
②由顶点
作四面体的高,其垂足是
的三条高线的交点;
③若分别作
和
的边
上的高,则这两条高所在直线异面;
④分别作三组相对棱中点的连线,所得的三条线段相交于一点;
⑤最长棱必有某个端点,由它引出的另两条棱的长度之和大于最长棱.
来源:2009年高考安徽卷理科数学第15题
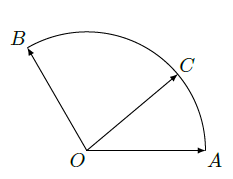
某地有 四人先后感染了甲型 流感,其中只有 到过疫区. 肯定是受 感染的.对于 ,因为难以断定他是受 还是受 感染的,于是假定他受 和受 感染的概率都是 .同样也假定 受 和 感染的概率都是 .在这种假定之下, 中直接受 感染的人数 就是一个随机变量.写出 的分布列(不要求写出计算过程),并求 的均值(即数学期望).
来源:2009年高考安徽卷理科数学第17题






 粤公网安备 44130202000953号
粤公网安备 44130202000953号