2022年广西北部湾经济区中考数学试卷
2022北京冬残奥会的会徽是以汉字“飞”为灵感来设计的,展现了运动员不断飞跃,超越自我,奋力拼搏,激励世界的冬残奥精神.下列的四个图中,能由如图所示的会徽经过平移得到的是( )

| A. |
|
B. |
|
C. |
|
D. |
|
空气由多种气体混合而成,为了直观介绍空气中各成分的百分比,最适合使用的统计图是( ).
| A. | 条形图 |
B. | 折线图 |
C. | 扇形图 |
D. | 直方图 |
如图,数轴上的点A表示的数是 ,则点A关于原点对称的点表示的数是( )
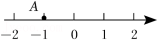
| A. | ﹣2 |
B. | 0 |
C. | 1 |
D. | 2 |
下列事件是必然事件的是( )
| A. |
三角形内角和是180° |
| B. |
端午节赛龙舟,红队获得冠军 |
| C. |
掷一枚均匀骰子,点数是6的一面朝上 |
| D. |
打开电视,正在播放神舟十四号载人飞船发射实况 |
如图,某博物馆大厅电梯的截面图中,AB的长为12米,AB与AC的夹角为α,则高BC是( )
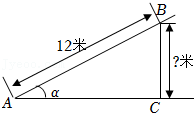
| A. | 米 |
B. | 米 |
C. | 米 |
D. | 米 |
《千里江山图》是宋代王希孟的作品,如图,它的局部画面装裱前是一个长为2.4米,宽为1.4米的矩形,装裱后,整幅图画宽与长的比是8:13,且四周边衬的宽度相等,则边衬的宽度应是多少米?设边衬的宽度为x米,根据题意可列方程( )

| A. |
|
B. |
|
| C. |
|
D. |
|
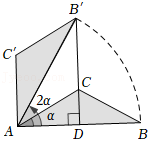
如图,在 中, , ,将 绕点A逆时针旋转 ,得到 ,连接 并延长交 于点 ,当 时, 的长是( )
| A. |
|
B. |
|
C. |
|
D. |
|
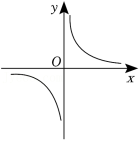
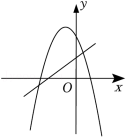
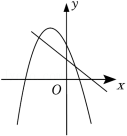
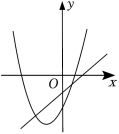
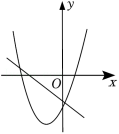
已知反比例函数 的图象如图所示,则一次函数 和二次函数 在同一平面直角坐标系中的图象可能是( )
| A. |
|
B. |
|
| C. |
|
D. |
|
如图,一个质地均匀的正五边形转盘,指针的位置固定,当转盘自由转动停止后,观察指针指向区域内的数(若指针正好指向分界线,则重新转一次),这个数是一个奇数的概率是 .
古希腊数学家泰勒斯曾利用立杆测影的方法,在金字塔影子的顶部直立一根木杆,借助太阳光测金字塔的高度.如图,木杆 长2米,它的影长 是4米,同一时刻测得 是268米,则金字塔的高度 是 米.

阅读材料:整体代值是数学中常用的方法.例如“已知 ,求代数式 的值.”可以这样解: .根据阅读材料,解决问题:若 是关于 的一元一次方程 的解,则代数式 的值是 .
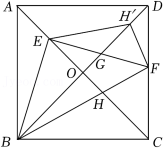
如图,在正方形 中, ,对角线 , 相交于点 .点 是对角线 上一点,连接 ,过点 作 ,分别交 , 于点 , ,连接 ,交 于点 ,将 沿 翻折,点 的对应点 恰好落在 上,得到 .若点 为 的中点,则 的周长是 .
如图,在 中,BD是它的一条对角线.
(1)求证: ;
(2)尺规作图:作BD的垂直平分线EF,分别交AD,BC于点E,F(不写作法,保留作图痕迹);
(3)连接BE,若 ,求 的度数.

综合与实践
【问题情境】数学活动课上,老师带领同学们开展“利用树叶的特征对树木进行分类”的实践活动.
【实践发现】同学们随机收集芒果树、荔枝树的树叶各10片,通过测量得到这些树叶的长y(单位:cm),宽x(单位:cm)的数据后,分别计算长宽比,整理数据如下:
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
芒果树叶的长宽比 |
3.8 |
3.7 |
3.5 |
3.4 |
3.8 |
4.0 |
3.6 |
4.0 |
3.6 |
4.0 |
荔枝树叶的长宽比 |
2.0 |
2.0 |
2.0 |
2.4 |
1.8 |
1.9 |
1.8 |
2.0 |
1.3 |
1.9 |
【实践探究】分析数据如下:
平均数 |
中位数 |
众数 |
方差 |
|
芒果树叶的长宽比 |
3.74 |
m |
4.0 |
0.0424 |
荔枝树叶的长宽比 |
1.91 |
1.95 |
n |
0.0669 |
【问题解决】
(1)上述表格中:m= ,n= ;
(2)①A同学说:“从树叶的长宽比的方差来看,我认为芒果树叶的形状差别大.”
②B同学说:“从树叶的长宽比的平均数、中位数和众数来看,我发现荔枝树叶的长约为宽的两倍.”
上面两位同学的说法中,合理的是 (填序号);
(3)现有一片长11cm,宽5.6cm的树叶,请判断这片树叶更可能来自于芒果、荔枝中的哪种树?并给出你的理由.
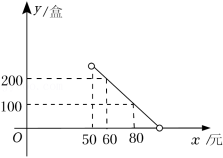
打油茶是广西少数民族特有的一种民俗.某特产公司近期销售一种盒装油茶,每盒的成本价为50元,经市场调研发现,该种油茶的月销售量y(盒)与销售单价x(元)之间的函数图象如图所示.
(1)求y与x的函数解析式,并写出自变量x的取值范围;
(2)当销售单价定为多少元时,该种油茶的月销售利润最大?求出最大利润.
如图,在 中, ,以AC为直径作⊙O交BC于点D,过点D作 ,垂足为E,延长BA交⊙O于点F.
(1)求证:DE是⊙O的切线;
(2)若 , ,求 的半径.
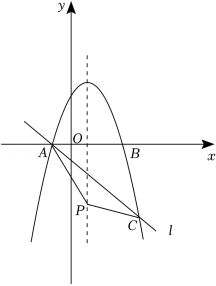
已知抛物线y=﹣x2+2x+3与x轴交于A,B两点(点A在点B的左侧).
(1)求点A,点B的坐标;
(2)如图,过点A的直线l:y=﹣x﹣1与抛物线的另一个交点为C,点P为抛物线对称轴上的一点,连接PA,PC,设点P的纵坐标为m,当PA=PC时,求m的值;
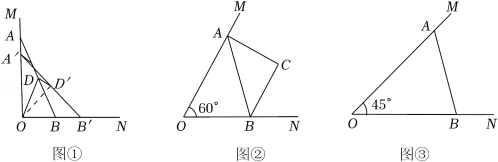
(3)将线段AB先向右平移1个单位长度,再向上平移5个单位长度,得到线段MN,若抛物线y=a(﹣x2+2x+3)(a≠0)与线段MN只有一个交点,请直接写出a的取值范围.





 粤公网安备 44130202000953号
粤公网安备 44130202000953号