2022年北京市中考数学试卷

下面几何体中，是圆锥的为（　　）

截至2021年12月31日，长江干流六座梯级水电站全年累计发电量达 $2628.83亿$千瓦时，相当于减排二氧化碳约 $2.2亿$吨．将 $262883000000$用科学记数法表示应为（　　）

如图，利用工具测量角，则 $\angle 1$的大小为（　　）

实数 $a，b$在数轴上的对应点的位置如图所示，下列结论中正确的是（　　）

不透明的袋子中装有红、绿小球各一个，除颜色外两个小球无其他差别．从中随机摸出一个小球，放回并摇匀，再从中随机摸出一个小球，那么第一次摸到红球、第二次摸到绿球的概率是（　　）

若关于 $x$的一元二次方程 $x^2+x+m＝0$有两个相等的实数根，则实数m的值为（　　）

图中的图形为轴对称图形，该图形的对称轴的条数为（　　）

下面的三个问题中都有两个变量：

①汽车从A地匀速行驶到B地，汽车的剩余路程y与行驶时间 $x$；

②将水箱中的水匀速放出，直至放完，水箱中的剩余水量 $y$与放水时间 $x$；

③用长度一定的绳子围成一个矩形，矩形的面积 $y$与一边长 $x$．

其中，变量 $y$与变量 $x$之间的函数关系可以用如图所示的图象表示的是（　　）

若 $\sqrt{x-8}$在实数范围内有意义，则实数 $x$的取值范围是＿＿＿＿＿．

分解因式： $x{y}^2﹣x＝$＿＿＿＿＿．

方程 $\frac{2}{x+5}=\frac{1}{x}$的解为＿＿＿＿＿．

在平面直角坐标系 $xOy$中，若点 $A（2，y_1），B（5，y_2）$在反比例函数 $y=\frac{k}{x}（k＞0）$的图象上，则 $y_1$＿＿＿＿＿ $y_2$（填“＞”“＝”或“＜”）．

某商场准备进 $400$双滑冰鞋，了解了某段时间内销售的 $40$双滑冰鞋的鞋号，数据如下：

根据以上数据，估计该商场进鞋号需求最多的滑冰鞋的数量为＿＿＿＿＿双．

如图，在△ABC中，AD平分 $\angle BAC$， $DE\perp AB$．若 $AC＝2，DE＝1$，则 $S_{△ACD}＝$＿＿＿＿＿．

如图，在矩形ABCD中，若 $AB＝3，AC＝5$， $\frac{\mathit{AF}}{\mathit{FC}}=\frac{1}{4}$，则AE的长为＿＿＿＿＿．

甲工厂将生产的Ⅰ号、Ⅱ号两种产品共打包成5个不同的包裹，编号分别为 $A，B，C，D，E，$每个包裹的重量及包裹中Ⅰ号、Ⅱ号产品的重量如下：

甲工厂准备用一辆载重不超过 $19.5$吨的货车将部分包裹一次运送到乙工厂．

（1）如果装运的Ⅰ号产品不少于 $9$吨，且不多于 $11$吨，写出一种满足条件的装运方案 　　＿＿＿＿＿（写出要装运包裹的编号）；

（2）如果装运的Ⅰ号产品不少于 $9$吨，且不多于 $11$吨，同时装运的Ⅱ号产品最多，写出满足条件的装运方案＿＿＿＿＿（写出要装运包裹的编号）．

计算： $（\pi ﹣1{）}^0+4\sin 45°-\sqrt{8}+|﹣3|$．

解不等式组： $\left\{\begin{array}{c}2+x＞7-4x，\\ x＜\frac{4+x}{2}．\end{array}\right.$．

已知 $x^2+2x﹣2＝0$，求代数式 $x（x+2）+（x+1{）}^2$的值．

下面是证明三角形内角和定理的两种添加辅助线的方法，选择其中一种，完成证明．

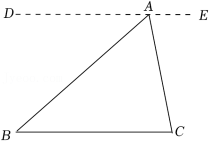
如图，在▱ABCD中，AC，BD交于点O，点E，F在AC上， $AE＝CF$．

（1）求证：四边形EBFD是平行四边形；

（2）若 $\angle BAC＝\angle DAC$，求证：四边形EBFD是菱形．

在平面直角坐标系 $xOy$中，函数 $y＝kx+b（k\ne 0）$的图象过点 $（4，3），（﹣2，0）$，且与 $y$轴交于点A．

（1）求该函数的解析式及点A的坐标；

（2）当 $x＞0$时，对于 $x$的每一个值，函数 $y＝x+n$的值大于函数 $y＝kx+b（k\ne 0）$的值，直接写出 $n$的取值范围．

某校举办“歌唱祖国”演唱比赛，十位评委对每位同学的演唱进行现场打分，对参加比赛的甲、乙、丙三位同学得分的数据进行整理、描述和分析．下面给出了部分信息．

a．甲、乙两位同学得分的折线图：

b．丙同学得分：

$10，10，10，9，9，8，3，9，8，10$

c．甲、乙、丙三位同学得分的平均数：

根据以上信息，回答下列问题：

（1）求表中 $m$的值；

（2）在参加比赛的同学中，如果某同学得分的10个数据的方差越小，则认为评委对该同学演唱的评价越一致．据此推断：在甲、乙两位同学中，评委对＿＿＿＿＿的评价更一致（填“甲”或“乙”）；

（3）如果每位同学的最后得分为去掉十位评委打分中的一个最高分和一个最低分后的平均分，最后得分越高，则认为该同学表现越优秀．据此推断：在甲、乙、丙三位同学中，表现最优秀的是 ＿＿＿＿＿（填“甲”“乙”或“丙”）．

如图，AB是⊙O的直径，CD是⊙O的一条弦， $AB\perp CD$，连接AC，OD．

（1）求证： $\angle BOD＝2\angle A$；

（2）连接DB，过点C作 $CE\perp DB$，交DB的延长线于点E，延长DO，交AC于点F．若F为AC的中点，求证：直线CE为⊙O的切线．

单板滑雪大跳台是北京冬奥会比赛项目之一，举办场地为首钢滑雪大跳台．运动员起跳后的飞行路线可以看作是抛物线的一部分．建立如图所示的平面直角坐标系，从起跳到着陆的过程中，运动员的竖直高度 $y$（单位： $m$）与水平距离 $x$（单位： $m$）近似满足函数关系 $y＝a（x﹣h{）}^2+k（a＜0）$．

某运动员进行了两次训练．

（1）第一次训练时，该运动员的水平距离 $x$与竖直高度 $y$的几组数据如下：

根据上述数据，直接写出该运动员竖直高度的最大值，并求出满足的函数关系 $y＝a（x﹣h{）}^2+k（a＜0）$；

（2）第二次训练时，该运动员的竖直高度 $y$与水平距离 $x$近似满足函数关系 $y＝﹣0.04（x﹣9{）}^2+23.24$．记该运动员第一次训练的着陆点的水平距离为 $d_1$，第二次训练的着陆点的水平距离为 $d_2$，则 $d_1$＿＿＿＿＿ $d_2$（填“＞”“＝”或“＜”）．

在平面直角坐标系 $xOy$中，点 $（1，m），（3，n）$在抛物线 $y＝a{x}^2+bx+c（a＞0）$上，设抛物线的对称轴为直线 $x＝t$．

（1）当 $c＝2，m＝n$时，求抛物线与 $y$轴交点的坐标及 $t$的值；

（2）点 $（x_0，m）（x_0\ne 1）$在抛物线上．若 $m＜n＜c$，求 $t$的取值范围及 $x_0$的取值范围．

在△ABC中， $\angle ACB＝90°$，D为△ABC内一点，连接BD，DC，延长DC到点E，使得 $CE＝DC$．

（1）如图1，延长BC到点F，使得 $CF＝BC$，连接AF，EF．若 $AF\perp EF$，求证： $BD\perp AF$；

（2）连接AE，交BD的延长线于点H，连接CH，依题意补全图2．若 $A{B}^2＝A{E}^2+B{D}^2$，用等式表示线段CD与CH的数量关系，并证明．

在平面直角坐标系xOy中，已知点 $M（a，b）$，N．

对于点P给出如下定义：将点P向右 $（a\ge 0）$或向左 $（a＜0）$平移 $\left|a\right|$个单位长度，再向上 $（b\ge 0）$或向下 $（b＜0）$平移 $\left|b\right|$个单位长度，得到点P′，点P′关于点N的对称点为Q，称点Q为点P的“对应点”．

（1）如图，点 $M（1，1）$，点N在线段OM的延长线上．若点 $P（﹣2，0）$，点Q为点P的“对应点”．

①在图中画出点Q；

②连接PQ，交线段ON于点T，求证： $NT=\frac{1}{2}OM$；

（2）⊙O的半径为 $1$，M是⊙O上一点，点N在线段OM上，且 $ON＝t（\frac{1}{2}＜t＜1）$，若P为⊙O外一点，点Q为点P的“对应点”，连接PQ．当点M在⊙O上运动时，直接写出PQ长的最大值与最小值的差（用含t的式子表示）．