2022年中考数学专题:三角形(二)
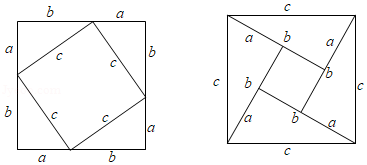
在勾股定理的学习过程中,我们已经学会了运用如图图形,验证著名的勾股定理,这种根据图形直观推论或验证数学规律和公式的方法,简称为"无字证明".实际上它也可用于验证数与代数,图形与几何等领域中的许多数学公式和规律,它体现的数学思想是
| A. |
统计思想 |
B. |
分类思想 |
C. |
数形结合思想 |
D. |
函数思想 |
阅读理解:如果一个正整数 能表示为两个正整数 , 的平方和,即 ,那么称 为广义勾股数,则下面的四个结论:①7不是广义勾股数;②13是广义勾股数;③两个广义勾股数的和是广义勾股数;④两个广义勾股数的积是广义勾股数.依次正确的是
| A. |
②④ |
B. |
①②④ |
C. |
①② |
D. |
①④ |
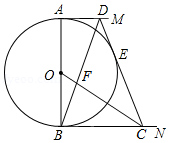
如图, 的直径 , , 是它的两条切线, 与 相切于点 ,并与 , 分别相交于 , 两点, , 相交于点 ,若 ,则 的长是
| A. |
|
B. |
|
C. |
|
D. |
|
如图,在 中, ,由图中的尺规作图痕迹得到的射线 与 交于点 ,点 为 的中点,连接 ,若 ,则 的周长为

| A. |
|
B. |
|
C. |
|
D. |
4 |
如图,在 中, , , ,按下列步骤作图:
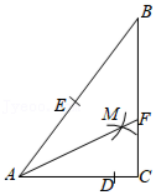
步骤1:以点 为圆心,小于 的长为半径作弧分别交 、 于点 、 .
步骤2:分别以点 、 为圆心,大于 的长为半径作弧,两弧交于点 .
步骤3:作射线 交 于点 .则 的长为
| A. |
6 |
B. |
|
C. |
|
D. |
|
如图是中国古代数学家赵爽用来证明勾股定理的弦图的示意图,它是由四个全等的直角三角形和一个小正方形 组成,恰好拼成一个大正方形 .连结 并延长交 于点 .若 , ,则 的长为

| A. |
|
B. |
|
C. |
|
D. |
|
如图,某港口 位于东西方向的海岸线上,甲、乙轮船同时离开港口,各自沿一固定方向航行,甲、乙轮船每小时分别航行12海里和16海里,1小时后两船分别位于点 , 处,且相距20海里,如果知道甲船沿北偏西 方向航行,则乙船沿 方向航行.

如图,正方形 的边长为4,对角线 , 相交于点 ,点 , 分别在 , 的延长线上,且 , , 为 的中点,连接 ,交 于点 ,连接 ,则 的长为 .

《九章算术》中一道"引葭赴岸"问题:"今有池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,问水深,葭长各几何?"题意是:有一个池塘,其地面是边长为10尺的正方形,一棵芦苇 生长在它的中央,高出水面部分 为1尺,如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部 恰好碰到岸边的 处(如图),水深和芦苇长各多少尺?则该问题的水深是 尺.

如图,正方形纸片 的边长为12,点 是 上一点,将 沿 折叠,点 落在点 处,连接 并延长交 于点 .若 ,则 的长为 .

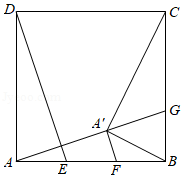
如图,在正方形 中, , 为边 上的两个三等分点,点 关于 的对称点为 , 的延长线交 于点 .
(1)求证: ;
(2)求 的大小;
(3)求证: .
已知 和 都是等腰直角三角形 , .
(1)如图1,连接 , ,求证: ;
(2)将 绕点 顺时针旋转.
①如图2,当点 恰好在 边上时,求证: ;
②当点 , , 在同一条直线上时,若 , ,请直接写出线段 的长.

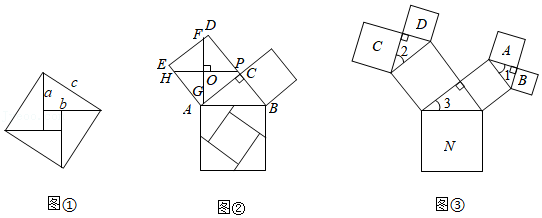
(1)阅读理解
我国是最早了解勾股定理的国家之一,它被记载于我国古代的数学著作《周髀算经》中.汉代数学家赵爽为了证明勾股定理,创制了一幅如图①所示的“弦图”,后人称之为“赵爽弦图”.
根据“赵爽弦图”写出勾股定理和推理过程;
(2)问题解决
勾股定理的证明方法有很多,如图②是古代的一种证明方法:过正方形 的中心 ,作 ,将它分成4份,所分成的四部分和以 为边的正方形恰好能拼成以 为边的正方形.若 , ,求 的值;
(3)拓展探究
如图③,以正方形一边为斜边向外作直角三角形,再以该直角三角形的两直角边分别向外作正方形,重复这一过程就可以得到“勾股树”的部分图形.设大正方形 的边长为定值 ,小正方形 , , , 的边长分别为 , , , .
已知 ,当角 变化时,探究 与 的关系式,并写出该关系式及解答过程 与 的关系式用含 的式子表示).
在一次数学探究活动中,李老师设计了一份活动单:
已知线段 ,使用作图工具作 ,尝试操作后思考: (1)这样的点 唯一吗? (2)点 的位置有什么特征?你有什么感悟? |
“追梦”学习小组通过操作、观察、讨论后汇报:点 的位置不唯一,它在以 为弦的圆弧上(点 、 除外), .小华同学画出了符合要求的一条圆弧(如图 .
(1)小华同学提出了下列问题,请你帮助解决.
①该弧所在圆的半径长为 ;
② 面积的最大值为 ;
(2)经过比对发现,小明同学所画的角的顶点不在小华所画的圆弧上,而在如图1所示的弓形内部,我们记为 ,请你根据图1证明 .
(3)请你运用所学知识,结合以上活动经验,解决问题:如图2,已知矩形 的边长 , ,点 在直线 的左侧,且 .
①线段 长的最小值为 ;
②若 ,则线段 长为 .

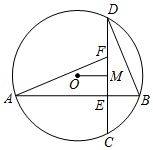
如图,圆 中两条互相垂直的弦 , 交于点 .
(1) 是 的中点, , ,求圆 的半径长;
(2)点 在 上,且 ,求证: .




 粤公网安备 44130202000953号
粤公网安备 44130202000953号