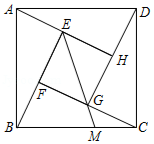
如图是中国古代数学家赵爽用来证明勾股定理的弦图的示意图,它是由四个全等的直角三角形和一个小正方形 组成,恰好拼成一个大正方形 .连结 并延长交 于点 .若 , ,则 的长为
| A. |
|
B. |
|
C. |
|
D. |
|
相关知识点
推荐套卷
如图是中国古代数学家赵爽用来证明勾股定理的弦图的示意图,它是由四个全等的直角三角形和一个小正方形 组成,恰好拼成一个大正方形 .连结 并延长交 于点 .若 , ,则 的长为

| A. |
|
B. |
|
C. |
|
D. |
|