2018年全国统一高考理科数学试卷(北京卷)
已知集合 , ,则 ( )
| A. | {0,1} |
B. | {−1,0,1} |
| C. | {−2,0,1,2} |
D. | {−1,0,1,2} |
在复平面内,复数 的共轭复数对应的点位于( )
| A. |
第一象限 |
B. |
第二象限 |
| C. |
第三象限 |
D. |
第四象限 |
"十二平均律" 是通用的音律体系,明代朱载堉最早用数学方法计算出半音比例,为这个理论的发展做出了重要贡献.十二平均律将一个纯八度音程分成十二份,依次得到十三个单音,从第二个单音起,每一个单音的频率与它的前一个单音的频率的比都等于 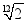 .若第一个单音的频率为 f ,则第八个单音的频率为( )
.若第一个单音的频率为 f ,则第八个单音的频率为( )
| A. |
|
B. |
|
| C. |
|
D. |
|
某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为( )

| A. |
1 |
B. |
2 |
| C. |
3 |
D. |
4 |
设向量 均为单位向量,则" "是" "的( )
| A. |
充分不必要条件 |
B. |
必要不充分条件 |
C. |
充要条件 |
D. |
既不充分又不必要条件 |
设集合 则( )
| A. |
对任意实数a, |
| B. |
对任意实数a,(2,1) |
| C. |
当且仅当a<0时,(2,1) |
| D. |
当且仅当 时,(2,1) |
能说明“若f(x)>f(0)对任意的x∈(0,2]都成立,则f(x)在[0,2]上是增函数”为假命题的一个函数是__________.
已知椭圆 ,双曲线 .若双曲线N的两条渐近线与椭圆M的四个交点及椭圆M的两个焦点恰为一个正六边形的顶点,则椭圆M的离心率为__________;双曲线N的离心率为__________.
如图,在三棱柱 ABC−
中,
平面 ABC, D, E, F, G分别为
, AC,
,  的中点, AB=BC=
, AC=
=2.
的中点, AB=BC=
, AC=
=2.
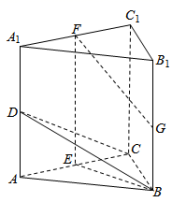
(1)求证: AC⊥平面 BEF;
(2)求二面角 B−CD− C 1的余弦值;
(3)证明:直线 FG与平面 BCD相交.
电影公司随机收集了电影的有关数据,经分类整理得到下表:
电影类型 |
第一类 |
第二类 |
第三类 |
第四类 |
第五类 |
第六类 |
电影部数 |
140 |
50 |
300 |
200 |
800 |
510 |
好评率 |
0.4 |
0.2 |
0.15 |
0.25 |
0.2 |
0.1 |
好评率是指:一类电影中获得好评的部数与该类电影的部数的比值.
假设所有电影是否获得好评相互独立.
(Ⅰ)从电影公司收集的电影中随机选取1部,求这部电影是获得好评的第四类电影的概率;
(Ⅱ)从第四类电影和第五类电影中各随机选取1部,估计恰有1部获得好评的概率;
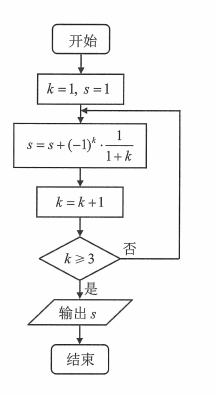
(Ⅲ)假设每类电影得到人们喜欢的概率与表格中该类电影的好评率相等,用" "表示第 k类电影得到人们喜欢," "表示第 k类电影没有得到人们喜欢( k=1,2,3,4,5,6).写出方差 , , , , , 的大小关系.
设函数 =[ ] .
(1)若曲线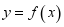 在点(1,
)处的切线与
轴平行,求
;
在点(1,
)处的切线与
轴平行,求
;
(2)若 在 处取得极小值,求 的取值范围.
已知抛物线C: =2px经过点 (1,2).过点Q(0,1)的直线l与抛物线C有两个不同的交点A,B,且直线PA交y轴于M,直线PB交y轴于N.
(Ⅰ)求直线l的斜率的取值范围;
(Ⅱ)设O为原点, , ,求证: 为定值.
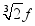
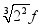
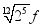
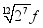
 粤公网安备 44130202000953号
粤公网安备 44130202000953号