2018年浙江省湖州市中考数学试卷
某工艺品厂草编车间共有16名工人,为了了解每个工人的日均生产能力,随机调查了某一天每个工人的生产件数.获得数据如下表:
生产件数(件 |
10 |
11 |
12 |
13 |
14 |
15 |
人数(人 |
1 |
5 |
4 |
3 |
2 |
1 |
则这一天16名工人生产件数的众数是
A.5件B.11件C.12件D.15件
某居委会组织两个检查组,分别对“垃圾分类”和“违规停车”的情况进行抽查.各组随机抽取辖区内某三个小区中的一个进行检查,则两个组恰好抽到同一个小区的概率是
A. B. C. D.
如图,已知在 中, ,点 为 的中点,点 在 上,将 沿 折叠,使得点 恰好落在 的延长线上的点 处,连接 ,则下列结论不一定正确的是
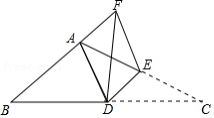
A. B.
C. 和 的面积相等D. 和 的面积相等
尺规作图特有的魅力曾使无数人沉湎其中.传说拿破仑通过下列尺规作图考他的大臣:
①将半径为 的 六等分,依次得到 , , , , , 六个分点;
②分别以点 , 为圆心, 长为半径画弧, 是两弧的一个交点;
③连接 .
问: 的长是多少?
大臣给出的正确答案应是

A. B. C. D.
在平面直角坐标系 中,已知点 , 的坐标分别为 , ,若抛物线 与线段 有两个不同的交点,则 的取值范围是
A. 或 B.
C. 或 D. 或
如图,在平面直角坐标系 中,已知抛物线 的顶点为 ,与 轴的正半轴交于点 ,它的对称轴与抛物线 交于点 .若四边形 是正方形,则 的值是 .

在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点.以顶点都是格点的正方形 的边为斜边,向内作四个全等的直角三角形,使四个直角顶点 , , , 都是格点,且四边形 为正方形,我们把这样的图形称为格点弦图.例如,在如图1所示的格点弦图中,正方形 的边长为 ,此时正方形 的面积为5.问:当格点弦图中的正方形 的边长为 时,正方形 的面积的所有可能值是 (不包括 .

某校积极开展中学生社会实践活动,决定成立文明宣传、环境保护、交通监督三个志愿者队伍,每名学生最多选择一个队伍,为了了解学生的选择意向,随机抽取 , , , 四个班,共200名学生进行调查.将调查得到的数据进行整理,绘制成如下统计图(不完整).

(1)求扇形统计图中交通监督所在扇形的圆心角度数;
(2)求 班选择环境保护的学生人数,并补全折线统计图;
(3)若该校共有学生2500人,试估计该校选择文明宣传的学生人数.
“绿水青山就是金山银山”,为了保护环境和提高果树产量,某果农计划从甲、乙两个仓库用汽车向 , 两个果园运送有机化肥,甲、乙两个仓库分别可运出80吨和100吨有机化肥; , 两个果园分别需用110吨和70吨有机化肥.两个仓库到 , 两个果园的路程如表所示:
路程(千米) |
||
甲仓库 |
乙仓库 |
|
果园 |
15 |
25 |
果园 |
20 |
20 |
设甲仓库运往 果园 吨有机化肥,若汽车每吨每千米的运费为2元,
(1)根据题意,填写下表.
运量(吨 |
运费(元 |
|||
甲仓库 |
乙仓库 |
甲仓库 |
乙仓库 |
|
果园 |
|
|
|
|
果园 |
|
|
|
|
(2)设总运费为 元,求 关于 的函数表达式,并求当甲仓库运往 果园多少吨有机化肥时,总运费最省?最省的总运费是多少元?
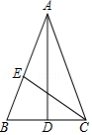
已知在 中, , , , 分别为 , 边上的点(不包括端点),且 ,连接 ,过点 作 ,垂足为点 ,延长 交 于点 .
(1)如图1,过点 作 于点 ,连接 .
①求证:四边形 是平行四边形;
②若 ,求证: ;
(2)如图2,若 ,求 的值.


 B.
B.
 D.
D.



 粤公网安备 44130202000953号
粤公网安备 44130202000953号