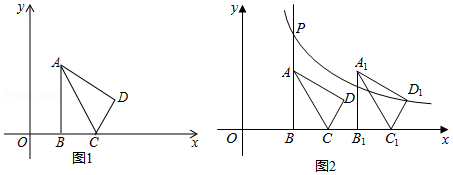
如图1,在平面直角坐标系 中,已知 , ,顶点 在第一象限, , 在 轴的正半轴上 在 的右侧), , , 与 关于 所在的直线对称.
(1)当 时,求点 的坐标;
(2)若点 和点 在同一个反比例函数的图象上,求 的长;
(3)如图2,将(2)中的四边形 向右平移,记平移后的四边形为 ,过点 的反比例函数 的图象与 的延长线交于点 .问:在平移过程中,是否存在这样的 ,使得以点 , , 为顶点的三角形是直角三角形?若存在,请直接写出所有符合题意的 的值;若不存在,请说明理由.
相关知识点
推荐套卷


 和
和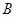 的距离.
的距离.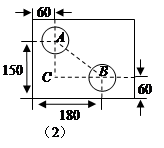
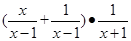 ,(2) 解方程:
,(2) 解方程: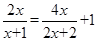 .
.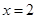 .
.
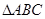 中,
中,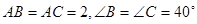 ,点
,点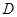 在线段
在线段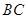 上运动(D不与B、C重合),连接AD,作
上运动(D不与B、C重合),连接AD,作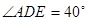 ,
,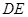 交线段
交线段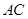 于
于 .
.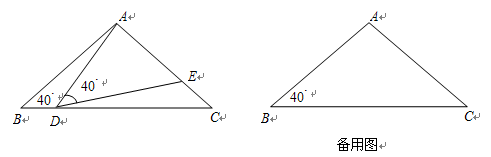
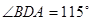 时,
时,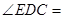 °,
°,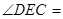 °;点D从B向C运动时,
°;点D从B向C运动时,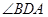 逐渐变(填“大”或“小”);
逐渐变(填“大”或“小”);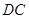 等于多少时,
等于多少时,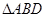 ≌
≌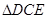 ,请说明理由;
,请说明理由;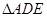 的形状可以是等腰三角形吗?若可以,请直接写出
的形状可以是等腰三角形吗?若可以,请直接写出 粤公网安备 44130202000953号
粤公网安备 44130202000953号