2018年山东省枣庄市中考数学试卷
已知直线 ,将一块含 角的直角三角板 按如图方式放置 ,其中 , 两点分别落在直线 , 上,若 ,则 的度数为

A. B. C. D.
如图,将边长为 的正方形沿虚线剪成两块正方形和两块长方形.若拿掉边长 的小正方形后,再将剩下的三块拼成一块矩形,则这块矩形较长的边长为

A. B. C. D.
如图是由8个全等的小矩形组成的大正方形,线段 的端点都在小矩形的顶点上,如果点 是某个小矩形的顶点,连接 、 ,那么使 为等腰直角三角形的点 的个数是

A.2个B.3个C.4个D.5个
如图,某商店营业大厅自动扶梯 的倾斜角为 , 的长为12米,则大厅两层之间的高度为 米.(结果保留两个有效数字)【参考数据; sin 31 ° = 0 . 515 , cos 31 ° = 0 . 857 , tan 31 ° = 0 . 601 】

我国南宋著名数学家秦九韶在他的著作《数书九章》一书中,给出了著名的秦九韶公式,也叫三斜求积公式,即如果一个三角形的三边长分别为 , , ,则该三角形的面积为 .现已知 的三边长分别为1,2, ,则 的面积为 .

如图,在正方形 中, ,把边 绕点 逆时针旋转 得到线段 ,连接 并延长交 于点 ,连接 ,则三角形 的面积为 .

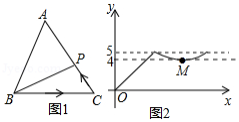
如图1,点 从 的顶点 出发,沿 匀速运动到点 ,图2是点 运动时,线段 的长度 随时间 变化的关系图象,其中 为曲线部分的最低点,则 的面积是 .
将从1开始的连续自然数按以下规律排列:
第1行 |
1 |
||||||||
第2行 |
2 |
3 |
4 |
||||||
第3行 |
9 |
8 |
7 |
6 |
5 |
||||
第4行 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
||
第5行 |
25 |
24 |
23 |
22 |
21 |
20 |
19 |
18 |
17 |
则2018在第 行.
如图,在 的方格纸中, 的三个顶点都在格点上.
(1)在图1中,画出一个与 成中心对称的格点三角形;
(2)在图2中,画出一个与 成轴对称且与 有公共边的格点三角形;
(3)在图3中,画出
绕着点
按顺时针方向旋转
后的三角形.
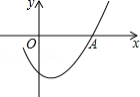
如图,一次函数 、 为常数, 的图象与 轴、 轴分别交于 、 两点,且与反比例函数 为常数,且 的图象在第二象限交于点 . 轴,垂足为 ,若 .
(1)求一次函数与反比例函数的解析式;
(2)记两函数图象的另一个交点为 ,求 的面积;
(3)直接写出不等式 的解集.

现今“微信运动”被越来越多的人关注和喜爱,某兴趣小组随机调查了我市50名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整)
步数 |
频数 |
频率 |
|
8 |
|
|
15 |
0.3 |
|
12 |
|
|
|
0.2 |
|
3 |
0.06 |
|
|
0.04 |
请根据以上信息,解答下列问题:
(1)写出 , , , 的值并补全频数分布直方图;
(2)本市约有37800名教师,用调查的样本数据估计日行走步数超过12000步(包含12000步)的教师有多少名?
(3)若在50名被调查的教师中,选取日行走步数超过16000步(包含16000步)的两名教师与大家分享心得,求被选取的两名教师恰好都在20000步(包含20000步)以上的概率.

如图,在 中, , , ,以 为直径作 交 于点 .
(1)求线段 的长度;
(2)点 是线段 上的一点,试问:当点 在什么位置时,直线 与 相切?请说明理由.

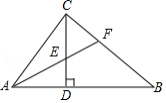
如图,将矩形 沿 折叠,使点 落在 边上的点 处,过点 作 交 于点 ,连接 .
(1)求证:四边形 是菱形;
(2)探究线段 、 、 之间的数量关系,并说明理由;
(3)若 , ,求 的长.






 粤公网安备 44130202000953号
粤公网安备 44130202000953号