2016年四川省成都市中考数学试卷
成都地铁自开通以来,发展速度不断加快,现已成为成都市民主要出行方式之一.今年4月29日成都地铁安全运输乘客约181万乘次,又一次刷新客流纪录,这也是今年以来第四次客流纪录的刷新,用科学记数法表示181万为
A. B. C. D.
学校准备从甲、乙、丙、丁四个科创小组中选出一组代表学校参加青少年科技创新大赛,各组的平时成绩的平均数 (单位:分)及方差 如表所示:
甲 |
乙 |
丙 |
丁 |
|
|
7 |
8 |
8 |
7 |
|
1 |
1.2 |
1 |
1.8 |
如果要选出一个成绩较好且状态稳定的组去参赛,那么应选的组是
A.甲B.乙C.丙D.丁
二次函数 的图象是一条抛物线,下列关于该抛物线的说法,正确的是
A.抛物线开口向下B.抛物线经过点
C.抛物线的对称轴是直线 D.抛物线与 轴有两个交点
在学习完“利用三角函数测高”这节内容之后,某兴趣小组开展了测量学校旗杆高度的实践活动,如图,在测点 处安置测倾器,量出高度 ,测得旗杆顶端 的仰角 ,量出测点 到旗杆底部 的水平距离 ,根据测量数据,求旗杆 的高度.(参考数据: , ,

在四张编号为 , , , 的卡片(除编号外,其余完全相同)的正面分别写上如图所示正整数后,背面朝上,洗匀放好,现从中随机抽取一张(不放回),再从剩下的卡片中随机抽取一张.

(1)请用树状图或列表的方法表示两次抽取卡片的所有可能出现的结果(卡片用 , , , 表示);
(2)我们知道,满足 的三个正整数 , , 成为勾股数,求抽到的两张卡片上的数都是勾股数的概率.
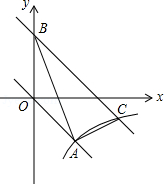
如图,在平面直角坐标 中,正比例函数 的图象与反比例函数 的图象都经过点 .
(1)分别求这两个函数的表达式;
(2)将直线 向上平移3个单位长度后与 轴交于点 ,与反比例函数图象在第四象限内的交点为 ,连接 , ,求点 的坐标及 的面积.
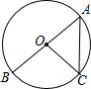
如图,在 中, ,以 为半径作 ,交 于点 ,交 的延长线于点 ,连接 , .
(1)求证: ;
(2)当 时,求 ;
(3)在(2)的条件下,作 的平分线,与 交于点 ,若 ,求 的半径.

第十二届全国人大四次会议审议通过的《中华人民共和国慈善法》将于今年9月1日正式实施,为了了解居民对慈善法的知晓情况,某街道办从辖区居民中随机选取了部分居民进行调查,并将调查结果绘制成如图所示的扇形图.若该辖区约有居民9000人,则可以估计其中对慈善法“非常清楚”的居民约有 人.

实数 , , , 满足 ,这四个数在数轴上对应的点分别为 , , , (如图),若 , ,则称 为 , 的“大黄金数”, 为 , 的“小黄金数”,当 时, , 的大黄金数与小黄金数之差 .
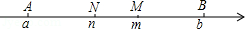
如图,面积为6的平行四边形纸片 中, , ,按下列步骤进行裁剪和拼图.

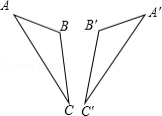
第一步:如图①,将平行四边形纸片沿对角线 剪开,得到 和 纸片,再将 纸片沿 剪开 为 上任意一点),得到 和 纸片;
第二步:如图②,将 纸片平移至 处,将 纸片平移至 处;
第三步:如图③,将 纸片翻转过来使其背面朝上置于 处(边 与 重合, 和 在 同侧),将 纸片翻转过来使其背面朝上置于 处,(边 与 重合, 和 在 同侧).
则由纸片拼成的五边形 中,对角线 长度的最小值为 .
某果园有100棵橙子树,平均每棵树结600个橙子,现准备多种一些橙子树以提高果园产量,但是如果多种树,那么树之间的距离和每一棵树所接受的阳光就会减少.根据经验估计,每多种一棵树,平均每棵树就会少结5个橙子,假设果园多种了 棵橙子树.
(1)直接写出平均每棵树结的橙子个数 (个 与 之间的关系;
(2)果园多种多少棵橙子树时,可使橙子的总产量最大?最大为多少个?
如图①, 中, , 于点 ,点 在 上,且 ,连接 .

(1)求证: ;
(2)将 绕点 旋转,得到 (点 , 分别与点 , 对应),连接 .
①如图②,当点 落在 上时, 不与 重合),若 , ,求 的长;
②如图③,当 是由 绕点 逆时针旋转 得到时,设射线 与 相交于点 ,连接 ,试探究线段 与 之间满足的等量关系,并说明理由.

 B.
B. C.
C. D.
D.




 粤公网安备 44130202000953号
粤公网安备 44130202000953号