2020年吉林省长春市中考数学试卷
为了增加青少年的校外教育活动场所,长春市将建成面积约为79000平方米的新少年宫,预计2020年12月正式投入使用.79000这个数用科学记数法表示为
| A. |
|
B. |
|
C. |
|
D. |
|
比萨斜塔是意大利的著名建筑,其示意图如图所示,设塔顶中心点为点 ,塔身中心线 与垂直中心线 的夹角为 ,过点 向垂直中心线 引垂线,垂足为点 .通过测量可得 、 、 的长度,利用测量所得的数据计算 的三角函数值,进而可求 的大小.下列关系式正确的是

| A. |
|
B. |
|
C. |
|
D. |
|
如图,在 中, , .按下列步骤作图:
①分别以点 和点 为圆心,大于 一半的长为半径作圆弧,两弧相交于点 和点 ;
②作直线 ,与边 相交于点 ,连结 .
下列说法不一定正确的是

| A. |
|
B. |
|
C. |
|
D. |
|
如图,在平面直角坐标系中,点 的坐标为 , 轴于点 ,点 是线段 上的点,连结 .点 在线段 上,且 ,函数 的图象经过点 .当点 在线段 上运动时, 的取值范围是

| A. |
|
B. |
|
C. |
|
D. |
|
长春市净月潭国家森林公园门票的价格为成人票每张30元,儿童票每张15元.若购买 张成人票和 张儿童票,则共需花费 元.
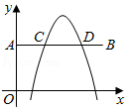
如图,在平面直角坐标系中,点 的坐标为 ,点 的坐标为 .若抛物线 、 为常数)与线段 交于 、 两点,且 ,则 的值为 .
现有三张不透明的卡片,其中两张卡片的正面图案为"神舟首飞",第三张卡片的正面图案为"保卫和平",卡片除正面图案不同外,其余均相同.将这三张卡片背面向上洗匀,从中随机抽取一张,记录图案后放回,重新洗匀后再从中随机抽取一张.请用画树状图(或列表)的方法,求两次抽出的卡片上的图案都是"保卫和平"的概率.(图案为"神舟首飞"的两张卡片分别记为 、 ,图案为"保卫和平"的卡片记为

图①、图②、图③均是 的正方形网格,每个小正方形的边长为1,每个小正方形的顶点称为格点,线段 的端点均在格点上,只用无刻度的直尺,在给定的网格中,按下列要求以 为边画 .
要求:
(1)在图①中画一个钝角三角形,在图②中画一个直角三角形,在图③中画一个锐角三角形;
(2)三个图中所画的三角形的面积均不相等;
(3)点 在格点上.

在国家精准扶贫的政策下,某村企生产的黑木耳获得了国家绿色食品标准认证,绿标的认证,使该村企的黑木耳在市场上更有竞争力,今年每斤黑木耳的售价比去年增加了20元.预计今年的销量是去年的3倍,年销售额为360万元.已知去年的年销售额为80万元,问该村企去年黑木耳的年销量为多少万斤?
空气质量按照空气质量指数大小分为六个级别,分别为:一级优、二级良、三级轻度污染、四级中度污染、五级重度污染、六级严重污染.级别越高,说明污染的情况越严重,对人体的健康危害也就越大.空气质量达到一级优或二级良的天气为达标天气,如图是长春市从2014年到2019年的空气质量级别天数的统计图表.
年长春市空气质量级别天数统计表
空气质量级别 天数 年份 |
优 |
良 |
轻度污染 |
中度污染 |
重度污染 |
严重污染 |
2014 |
30 |
215 |
73 |
28 |
13 |
6 |
2015 |
43 |
193 |
87 |
19 |
15 |
8 |
2016 |
51 |
237 |
58 |
15 |
5 |
0 |
2017 |
65 |
211 |
62 |
16 |
9 |
2 |
2018 |
123 |
202 |
39 |
0 |
1 |
0 |
2019 |
126 |
180 |
38 |
16 |
5 |
0 |
根据上面的统计图表回答下列问题:
(1)长春市从2014年到2019年空气质量为"达标"的天数最多的是 年.
(2)长春市从2014年到2019年空气质量为"重度污染"的天数的中位数为 天,平均数为 天.
(3)长春市从2015年到2019年,和前一年相比,空气质量为"优"的天数增加最多的是 年,这一年空气质量为"优"的天数的年增长率约为 (精确到 .
(空气质量为"优"的天数的增长率
(4)你认为长春市从2014年到2019年哪一年的空气质量好?请说明理由.

已知 、 两地之间有一条长240千米的公路.甲车从 地出发匀速开往 地,甲车出发两小时后,乙车从 地出发匀速开往 地,两车同时到达各自的目的地.两车行驶的路程之和 (千米)与甲车行驶的时间 (时 之间的函数关系如图所示.
(1)甲车的速度为 千米 时, 的值为 .
(2)求乙车出发后, 与 之间的函数关系式.
(3)当甲、乙两车相距100千米时,求甲车行驶的时间.

【教材呈现】如图是华师版八年级下册数学教材第121页的部分内容.
1.把一张矩形纸片如图那样折一下,就可以裁出正方形纸片,为什么?
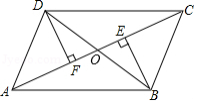
【问题解决】如图①,已知矩形纸片 ,将矩形纸片沿过点 的直线折叠,使点 落在边 上,点 的对应点为 ,折痕为 ,点 在 上.求证:四边形 是正方形.
【规律探索】由【问题解决】可知,图①中的△ 为等腰三角形.现将图①中的点 沿 向右平移至点 处(点 在点 的左侧),如图②,折痕为 ,点 在 上,点 在 上,那么 还是等腰三角形吗?请说明理由.
[结论应用]在图②中,当 时,将矩形纸片继续折叠如图③,使点 与点 重合,折痕为 ,点 在 上.要使四边形 为菱形,则 .


如图①,在 中, , , .点 从点 出发,沿折线 以每秒5个单位长度的速度向点 运动,同时点 从点 出发,沿 以每秒2个单位长度的速度向点 运动,点 到达点 时,点 、 同时停止运动.当点 不与点 、 重合时,作点 关于直线 的对称点 ,连结 交 于点 ,连结 、 .设点 的运动时间为 秒.
(1)当点 与点 重合时,求 的值.
(2)用含 的代数式表示线段 的长.
(3)当 为锐角三角形时,求 的取值范围.
(4)如图②,取 的中点 ,连结 .当直线 与 的一条直角边平行时,直接写出 的值.












 粤公网安备 44130202000953号
粤公网安备 44130202000953号