2019年陕西省中考数学试卷
如图,在矩形 中, , ,若点 , 分别在 , 上,且 , , , 分别是 的三等分点,则四边形 的面积为

| A. |
1 |
B. |
|
C. |
2 |
D. |
4 |
本学期初,某校为迎接中华人民共和国建国七十周年,开展了以“不忘初心,缅怀革命先烈,奋斗新时代”为主题的读书活动.校德育处对本校七年级学生四月份“阅读该主题相关书籍的读书量”(下面简称:“读书量” 进行了随机抽样调查,并对所有随机抽取学生的“读书量”(单位:本)进行了统计,如图所示:

根据以上信息,解答下列问题:
(1)补全上面两幅统计图,填出本次所抽取学生四月份“读书量”的众数为 .
(2)求本次所抽取学生四月份“读书量”的平均数;
(3)已知该校七年级有1200名学生,请你估计该校七年级学生中,四月份“读书量”为多杀本的学生人数.
小明利用刚学过的测量知识来测量学校内一棵古树的高度.一天下午,他和学习小组的同学带着测量工具来到这棵古树前,由于有围栏保护,他们无法到达古树的底部,如图所示.于是他们先在古树周围的空地上选择一点,并在点处安装了测量器,测得古树的顶端的仰角为;再在的延长线上确定一点,使米,并在处的地面上水平放置了一个小平面镜,小明沿着方向移动,当移动到点时,他刚好在小平面镜内看到这棵古树的顶端的像,此时,测得米,小明眼睛与地面的距离米,测倾器的高度米.已知点、、、在同一水平直线上,且、、均垂直于,求这棵古树的高度.(小平面镜的大小忽略不计)

根据记录,从地面向上以内,每升高,气温降低;又知在距离地面以上高空,气温几乎不变.若地面气温为,设距地面的高度为处的气温为
(1)写出距地面的高度在以内的与之间的函数表达式;
(2)上周日,小敏在乘飞机从上海飞回西安途中,某一时刻,她从机舱内屏幕显示的相关数据得知,飞机外气温为时,飞机距离地面的高度为,求当时这架飞机下方地面的气温;小敏想,假如飞机当时在距离地面的高空,飞机外的气温是多少度呢?请求出假如当时飞机距离地面时,飞机外的气温.
现有、两个不透明袋子,分别装有3个除颜色外完全相同的小球.其中,袋装有2个白球,1个红球;袋装有2个红球,1个白球.
(1)将袋摇匀,然后从袋中随机取出一个小球,求摸出小球是白色的概率;
(2)小华和小林商定了一个游戏规则:从摇匀后的,两袋中随机摸出一个小球,摸出的这两个小球,若颜色相同,则小林获胜;若颜色不同,则小华获胜.请用列表法或画出树状图的方法说明这个游戏规则对双方是否公平.
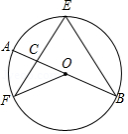
如图,是的直径,是的一条弦,是的切线.作并与交于点,延长交于点,交于点,连接.
(1)求证:;
(2)若的半径,,求的长.

在平面直角坐标系中,已知抛物线经过点和点,关于原点对称的抛物线为.
(1)求抛物线的表达式;
(2)点在抛物线上,且位于第一象限,过点作轴,垂足为.若与相似,求符合条件的点的坐标.

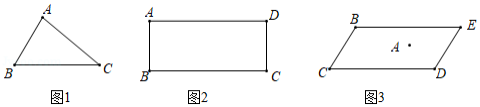
问题提出:
(1)如图1,已知,试确定一点,使得以,,,为顶点的四边形为平行四边形,请画出这个平行四边形;
问题探究:
(2)如图2,在矩形中,,,若要在该矩形中作出一个面积最大的,且使,求满足条件的点到点的距离;
问题解决:
(3)如图3,有一座塔,按规定,要以塔为对称中心,建一个面积尽可能大的形状为平行四边形的景区.根据实际情况,要求顶点是定点,点到塔的距离为50米,,那么,是否可以建一个满足要求的面积最大的平行四边形景区?若可以,求出满足要求的平行四边形的最大面积;若不可以,请说明理由.(塔的占地面积忽略不计)











 粤公网安备 44130202000953号
粤公网安备 44130202000953号