2019年陕西省中考数学试卷（副卷）

$-8$ 的立方根是 $($ 　　 $)$

如图，是由两个大小不同的长方体组成的几何体，则该几何体的主视图为 $($ 　　 $)$

如图，在 $\mathit{\Delta ABC}$ 中， $\angle A=46°$ ， $\angle B=72°$ ．若直线 $l//\mathit{BC}$ ，则 $\angle 1$ 的度数为 $($ 　　 $)$

$A\text{'}$ 是点 $A(1,2)$ 关于 $x$ 轴的对称点．若一个正比例函数的图象经过点 $A\text{'}$ ，则该函数的表达式为 $($ 　　 $)$

下列计算正确的是 $($ 　　 $)$

如图，在 $\mathit{\Delta ABC}$ 中， $\angle \mathit{ABC}=90°$ ， $\angle C=52°$ ， $\mathit{BE}$ 为 $\mathit{AC}$ 边上的中线， $\mathit{AD}$ 平分 $\angle \mathit{BAC}$ ，交 $\mathit{BC}$ 边于点 $D$ ，过点 $B$ 作 $\mathit{BF}\perp \mathit{AD}$ ，垂足为 $F$ ，则 $\angle \mathit{EBF}$ 的度数为 $($ 　　 $)$

若直线 $y=\mathit{kx}+b(k\ne 0)$ 经过点 $A(2,-3)$ ，且与 $y$ 轴的交点在 $x$ 轴上方，则 $k$ 的取值范围是 $($ 　　 $)$

如图，在矩形 $\mathit{ABCD}$ 中， $\mathit{AB}=6$ ， $\mathit{BC}=8$ ，过矩形的对称中心 $O$ 的直线 $\mathit{EF}$ ，分别与 $\mathit{AD}$ 、 $\mathit{BC}$ 交于点 $E$ 、 $F$ ，且 $\mathit{FC}=2$ ．若 $H$ 为 $\mathit{OE}$ 的中点，连接 $\mathit{BH}$ 并延长，与 $\mathit{AD}$ 交于点 $G$ ，则 $\mathit{BG}$ 的长为 $($ 　　 $)$

如图， $\odot O$ 的半径为5， $\mathit{\Delta ABC}$ 内接于 $\odot O$ ，且 $\mathit{BC}=8$ ， $\mathit{AB}=\mathit{AC}$ ，点 $D$ 在 $\stackrel{̂}{\mathit{AC}}$ 上．若 $\angle \mathit{AOD}=\angle \mathit{BAC}$ ，则 $\mathit{CD}$ 的长为 $($ 　　 $)$

在平面直角坐标系中，将抛物线 $y=x^2-(a-2)x+a^2-1$ 向右平移4个单位长度，平移后的抛物线与 $y$ 轴的交点为 $A(0,3)$ ，则平移后的抛物线的对称轴为 $($ 　　 $)$

比较大小：$3\sqrt{3}$　　$2\sqrt{7}$．

如图，正五边形$\mathit{ABCDE}$的边长为1，对角线$\mathit{AC}$、$\mathit{BE}$相交于点$O$，则四边形$\mathit{OCDE}$的周长为　．

如图，在平面直角坐标系中，正方形$\mathit{OABC}$的面积为4，边$\mathit{OA}$、$\mathit{OC}$分别在$x$轴、$y$轴上，一个反比例函数的图象经过点$B$．若该函数图象上的点$P$到$y$轴的距离是这个正方形边长的一半，则点$P$的坐标为　　．

如图，$O$为菱形$\mathit{ABCD}$的对称中心，$\mathit{AB}=4$，$\angle \mathit{BAD}=120°$．若点$E$、$F$分别在$\mathit{AB}$、$\mathit{BC}$边上，连接$\mathit{OE}$、$\mathit{OF}$，则$\mathit{OE}+\mathit{OF}$的最小值为　　．

计算： $-2\times {\left(\sqrt{3}\right)}^2+|\sqrt{5}-3|-{(-65)}^0$ ．

解方程： $\frac{5x-8}{x^2-9}-1=\frac{3-x}{x+3}$ ．

如图，已知$\angle \mathit{AOB}$，点$M$在边$\mathit{OA}$上．请用尺规作图法求作$\odot M$，使$\odot M$与边$\mathit{OB}$相切．（保留作图痕迹，不写作法）

如图，在$\mathit{\Delta ABC}$中，$D$是$\mathit{BC}$边的中点，过点$D$作$\mathit{DE}//\mathit{AB}$，并与$\mathit{AC}$交于点$E$，延长$\mathit{DE}$到点$F$，使得$\mathit{EF}=\mathit{DE}$，连接$\mathit{AF}$．

求证：$\mathit{AF}//\mathit{BC}$．

今年植树节，某校开展了“植树造林，从我做起”的植树活动．该校参加本次植树活动的全体学生被分成了115个植树小组，按学校要求，每个植树小组至少植树10棵．经过一天的植树活动，校团委为了了解本次植树任务的完成情况，从这115个植树小组中随机抽查了10个小组，并对这10个小组植树的棵数进行了统计，结果如下：

根据以上提供的信息，解答下列问题：

（1）求所统计的这组数据的中位数和平均数；

（2）求抽查的这10个小组中，完成本次植树任务的小组所占的百分比；

（3）请你估计在本次植树活动中，该校学生共植树多少棵．

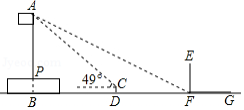
新学期，小华和小明被选为升旗手，为了更好地完成升旗任务，他俩想利用测倾器和阳光下的影子来测量学校旗杆的高度$\mathit{PA}$．如图所示，旗杆直立于旗台上的点$P$处，他们的测量方法是：首先，在阳光下，小华站在旗杆影子的顶端$F$处，此时，量得小华的影长$\mathit{FG}=2m$，小华身高$\mathit{EF}=1.6m$；然后，在旗杆影子上的点$D$处，安装测倾器$\mathit{CD}$，测得旗杆顶端$A$的仰角为$49°$，量得$\mathit{CD}=0.6m$，$\mathit{DF}=6m$，旗台高$\mathit{BP}=1.2m$．已知在测量过程中，点$B$、$D$、$F$、$G$在同一水平直线上，点$A$、$P$、$B$在同一条直线上，$\mathit{AB}$、$\mathit{CD}$、$\mathit{EF}$均垂直于$\mathit{BG}$．求旗杆的高度$\mathit{PA}$．（参考数据：$\sin 49°\approx 0.8$，$\cos 49°\approx 0.7$，$\tan 49°\approx 1.2)$

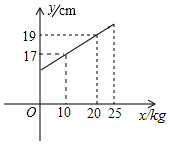
在所挂物体质量不超过$25\mathit{kg}$时，一弹簧的长度$y\left(\mathit{cm}\right)$是所挂物体质量$x\left(\mathit{kg}\right)$的一次函数，其图象如图所示．

（1）求$y$与$x$之间的函数表达式及该弹簧不挂物体时的长度；

（2）若该弹簧挂上一个物体后，弹簧长度为$16\mathit{cm}$，求这个物体的质量．

从同一副扑克牌中选出7张，分为$A$、$B$两组，其中$A$组是三张牌，牌面数字分别为1，2，3；$B$组是四张牌，牌面数字分别为5，6，7，8．

（1）将$A$组牌的背面都朝上，洗匀，随机抽出一张，求抽出的这张牌的牌面数字是3的概率；

（2）小亮与小涛商定了一个游戏规则：分别将$A$、$B$两组牌的背面都朝上，洗匀，再分别从$A$、$B$两组牌中各随机抽出一张，将这两张牌的牌面数字相加，若和为偶数，则小亮获胜；若和为奇数，则小涛获胜．请用列表或画树状图的方法说明这个游戏规则对双方是否公平．

如图，$\odot O$的半径$\mathit{OA}=6$，过点$A$作$\odot O$的切线$\mathit{AP}$，且$\mathit{AP}=8$，连接$\mathit{PO}$并延长，与$\odot O$交于点$B$、$D$，过点$B$作$\mathit{BC}//\mathit{OA}$，并与$\odot O$交于点$C$，连接$\mathit{AC}$、$\mathit{CD}$．

（1）求证：$\mathit{DC}//\mathit{AP}$；

（2）求$\mathit{AC}$的长．

在平面直角坐标系中，抛物线$L$经过点$A(-1,0)$，$B(3,0)$，$C(1,-2)$．

（1）求抛物线$L$的表达式；

（2）连接$\mathit{AC}$、$\mathit{BC}$．以点$D(1,2)$为位似中心，画△$A\text{'}B\text{'}C\text{'}$，使它与$\mathit{\Delta ABC}$位似，且相似比为2，$A\text{'}$、$B\text{'}$、$C\text{'}$分别是点$A$、$B$、$C$的对应点．试判定是否存在满足条件的点$A\text{'}$、$B\text{'}$在抛物线$L$上？若存在，求点$A\text{'}$、$B\text{'}$的坐标；若不存在，请说明理由．

问题提出

（1）如图①，已知直线$l$及$l$外一点$A$，试在直线$l$上确定$B$、$C$两点，使$\angle \mathit{BAC}=90°$，并画出这个$\text{Rt}\Delta \text{ABC}$．

问题探究

（2）如图②，$O$是边长为28的正方形$\mathit{ABCD}$的对称中心，$M$是$\mathit{BC}$边上的中点，连接$\mathit{OM}$．试在正方形$\mathit{ABCD}$的边上确定点$N$，使线段$\mathit{ON}$和$\mathit{OM}$将正方形$\mathit{ABCD}$分割成面积之比为$1:6$的两部分．求点$N$到点$M$的距离．

问题解决

（3）如图③，有一个矩形花园$\mathit{ABCD}$，$\mathit{AB}=30m$，$\mathit{BC}=40m$．根据设计要求，点$E$、$F$在对角线$\mathit{BD}$上，且$\angle \mathit{EAF}=60°$，并在四边形区域$\mathit{AECF}$内种植一种红色花卉，在矩形内其他区域均种植一种黄色花卉．已知种植这种红色花卉每平方米需210元，种植这种黄色花卉每平方米需180元．试求按设计要求，完成这两种花卉的种植至少需费用多少元？（结果保留整数．参考数据：$\sqrt{2}\approx 1.4$，$\sqrt{3}\approx 1.7)$