2015年全国统一高考理科数学试卷(陕西卷)
某中学初中部共有110名教师,高中部共有150名教师,其性别比例如图所示,则该校女教师的人数为()

| A. | 167 | B. | 137 | C. | 123 | D. | 93 |
如图,某港口一天6时到18时的水深变化曲线近似满足函数 ,据此函数可知,这段时间水深(单位: )的最大值为()

| A. | 5 | B. | 6 | C. | 8 | D. | 10 |
某企业生产甲、乙两种产品均需用
两种原料.已知生产1吨每种产品需原料及每天原料的可用限额如表所示,如果生产1吨甲、乙产品可获利润分别为3万元、4万元,则该企业每天可获得最大利润为( )

| A. | 12万元 |
B. | 16万元 |
C. | 17万元 |
D. | 18万元 |
对二次函数(为非零常数),四位同学分别给出下列结论,其中有且仅有一个结论是错误的,则错误的结论是()
| A. | 是 的零点 | B. | 1是 的极值点 |
| C. | 3是 的极值 | D. | 点 在曲线 上 |
如图,一横截面为等腰梯形的水渠,因泥沙沉积,导致水渠截面边界呈抛物线型(图中虚线表示),则原始的最大流量与当前最大流量的比值为 .

如图  ,在直角梯形
中,
,
,
,
,
,在直角梯形
中,
,
,
,
,  是
的中点,
是
与
的交点.将
沿
折起到
的位置,如图
是
的中点,
是
与
的交点.将
沿
折起到
的位置,如图  .
.

(Ⅰ)证明:
平面
;
(Ⅱ)若平面
平面
,求平面
与平面
夹角的余弦值.
设某校新、老校区之间开车单程所需时间为 , 只与道路畅通状况有关,对其容量为 的样本进行统计,结果如下:

(Ⅰ)求
的分布列与数学期望
;
(Ⅱ)刘教授驾车从老校区出发,前往新校区做一个50分钟的讲座,结束后立即返回老校区,求刘教授从离开老校区到返回老校区共用时间不超过120分钟的概率.
已知椭圆
的半焦距为
,原点
到经过两点
的直线的距离为
.
(Ⅰ)求椭圆
的离心率;
(Ⅱ)如图,
是圆
的一条直径,若椭圆
经过
两点,求椭圆
的方程.

设是等比数列 ,,的各项和,其中,
,,的各项和,其中,
(Ⅰ)证明:函数在内有且仅有一个零点(记为),且;
(Ⅱ)设有一个与上述等比数列的首项、末项、项数分别相同的等差数列,其各项和为,比较与 的大小,并加以证明.
的大小,并加以证明.
如图,
切
于点  ,直线
交
于
,
,直线
交
于
,  两点,
,垂足为
.
两点,
,垂足为
.

(Ⅰ)证明:
;
(Ⅱ)若
,
,求
的直径.
在直角坐标系中,直线的参数方程为(为参数).以原点为极点,轴正半轴为极轴建立极坐标系.的极坐标方程为.
(Ⅰ)写出的直角坐标方程;
(Ⅱ)为直线上一动点,当到圆心的距离最小时,求的直角坐标.

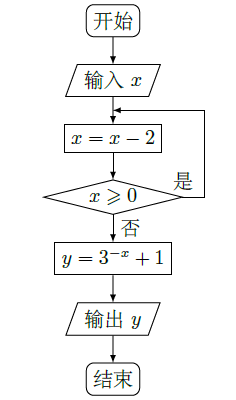
 时,输出的
()
时,输出的
()
 粤公网安备 44130202000953号
粤公网安备 44130202000953号