小光准备从 地去往 地,打开导航、显示两地距离为 ,但导航提供的三条可选路线长却分别为 , , (如图).能解释这一现象的数学知识是
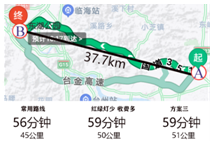
| A. |
两点之间,线段最短 |
B. |
垂线段最短 |
| C. |
三角形两边之和大于第三边 |
D. |
两点确定一条直线 |
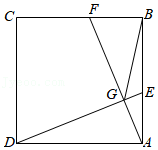
如图,在正方形 中, , 为边 上一点, 为边 上一点.连接 和 交于点 ,连接 .若 ,则 的最小值为 .
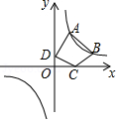
我们知道,两点之间线段最短,因此,连接两点间线段的长度叫做两点间的距离;同理,连接直线外一点与直线上各点的所有线段中,垂线段最短,因此,直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.类似地,连接曲线外一点与曲线上各点的所有线段中,最短线段的长度,叫做点到曲线的距离.依此定义,如图,在平面直角坐标系中,点 到以原点为圆心,以1为半径的圆的距离为 .

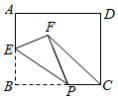
如图,在矩形 中, 为 的中点, 为 边上的任意一点,把 沿 折叠,得到 ,连接 .若 , ,则 的最小值为 .
如图,正方形 中, , 是 边的中点,点 是正方形内一动点, ,连接 ,将线段 绕点 逆时针旋转 得 ,连接 , .

(1)求证: ;
(2)若 , , 三点共线,连接 ,求线段 的长.
(3)求线段 长的最小值.
如图,在 中,直径
中,直径 垂直于不过圆心
垂直于不过圆心 的弦
的弦 ,垂足为点
,垂足为点 ,连接
,连接 ,点
,点 在
在 上,且
上,且
(1)求证: ;
;
(2)过点 作
作 的切线交
的切线交 的延长线于点
的延长线于点 ,试判断
,试判断 与
与 是否相等,并说明理由;
是否相等,并说明理由;
(3)设 半径为4,点
半径为4,点 为
为 中点,点
中点,点 在
在 上,求线段
上,求线段 的最小值.
的最小值.

某同学用剪刀沿直线将一片平整的银杏叶剪掉一部分(如图),发现剩下的银杏叶的周长比原银杏叶的周长要小,能正确解释这一现象的数学知识是

A.两点之间线段最短
B.两点确定一条直线
C.垂线段最短
D.经过直线外一点,有且只有一条直线与这条直线平行
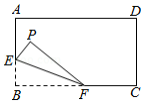
如图,矩形 中, , , 是 上一点,且 , 是 上一动点,若将 沿 对折后,点 落在点 处,则点 到点 的最短距离为 .
如图,点 , 都在双曲线 上,点 , ,分别是 轴, 轴上的动点,则四边形 周长的最小值为
A. B. C. D.
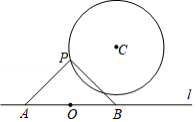
如图,已知 的半径为3,圆外一定点 满足 ,点 为 上一动点,经过点 的直线 上有两点 、 ,且 , , 不经过点 ,则 的最小值为 .
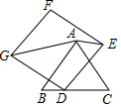
如图, 是等边三角形,点 为 边上一点, ,以点 为顶点作正方形 ,且 ,连接 , .若将正方形 绕点 旋转一周,当 取最小值时, 的长为 .
如图,在矩形 中, , , 是 边的中点, 是 边上的动点,将 沿 所在直线折叠,得到△ ,连接 ,则 的最小值是 .
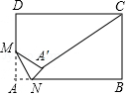
如图,在矩形纸片 中, , ,点 是 的中点,点 是 边上的一个动点,将 沿 所在直线翻折,得到△ ,则 的长的最小值是 .

如图,在 中, , , ,点 是 的三等分点,半圆 与 相切, , 分别是 与半圆弧上的动点,则 的最小值和最大值之和是
A.5B.6C.7D.8