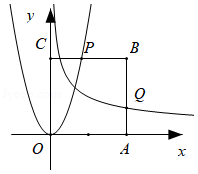
如图,已知正方形 ,其中 ,函数 交 于点 ,函数 交 于点 ,当 最小时,则 的值为________.
设函数 为 的导函数.
(Ⅰ)求 的单调区间;
(Ⅱ)当 时,证明 ;
(Ⅲ)设 为函数 在区间 内的零点,其中 ,证明 .
设 ,则" "是" "的( )
| A. |
充分而不必要条件 |
B. |
必要而不充分条件 |
| C. |
充要条件 |
D. |
既不充分也不必要条件 |
设变量 满足约束条件 ,则目标函数 的最大值为( )
| A. |
2 |
B. |
3 |
C. |
5 |
D. |
6 |
李明自主创业,在网上经营一家水果店,销售的水果中有草莓、京白梨、西瓜、桃,价格依次为60元/盒、65元/盒、80元/盒、90元/盒.为增加销量,李明对这四种水果进行促销:一次购买水果的总价达到120元,顾客就少付 元.每笔订单顾客网上支付成功后,李明会得到支付款的80%.
①当 时,顾客一次购买草莓和西瓜各1盒,需要支付__________元;
②在促销活动中,为保证李明每笔订单得到的金额均不低于促销前总价的七折,则 的最大值为__________.
若 x, y满足 则 的最小值为__________,最大值为__________.
已知x,y满足约束条件 ,则 的最大值是( )
| A. |
0 |
B. |
2 |
C. |
5 |
D. |
6 |
在平面直角坐标系
中,P是曲线
上的一个动点,则点P到直线x+y=0的距离的最小值是________.
命题p:关于x的不等式x2+2ax+4>0,对一切x∈R恒成立,命题q:指数函数f(x)=(3﹣2a)x是增函数,若p∨q为真,p∧q为假,求实数a的取值范围.