初中物理杠杆的平衡条件计算题

某工地施工时，用固定在水平工作台上的卷扬机（其内部有电动机提供动力）通过滑轮组提升货物如图甲所示，卷扬机及其工作台的总重为500N。为监测卷扬机的工作情况，将固定卷扬机的工作台置于水平轻质杠杆的A端，地面上的重为400N配重C与杠杆B端相连接，杠杆AB可绕转轴O在竖直平面内自由转动。当卷扬机以速度v₁匀速提升重为G₁=800N的货物上升时，卷扬机的拉力为F₁，配重C对地面的压强为p₁，滑轮组的机械效率为η₁；当卷扬机以速度v₂匀速提升重为G₂的货物上升时，卷扬机的拉力为F₂，配重C对地面的压强为p₂，滑轮组的机械效率为η₂；卷扬机的拉力F₁、F₂做功随时间变化的图像分别如图乙中①、②所示。已知：υ₁:υ₂ =1:3, η₁:η₂=16:15， OA:OB=2:5。忽略所有连接绳索的质量及各处摩擦。G取10N/kg.求：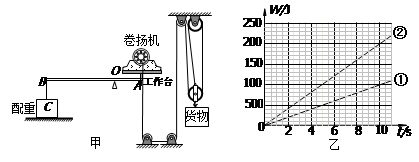

（1）卷扬机提升重物G₁上升12s做的功；
（2）动滑轮的质量；
（3）p₁与p₂的比值。

如图所示是某科技小组设计的打捞水中物体的装置示意图。A是动滑轮，B是定滑轮，C是卷扬机。卷扬机转动拉动钢丝绳通过滑轮组AB竖直提升水中的物体。在一次模拟打捞水中物体的作业中，在物体浸没水中匀速上升的过程中，船浸入水中的体积相对于动滑轮A未挂物体时变化了2dm3；在物体全部露出水面匀速上升的过程中，船浸入水中的体积相对于动滑轮A未挂物体时变化了3dm3，卷扬机所做的功随时间变化的图像如图2所示。物体浸没在水中和完全露出水面后卷扬机对钢丝绳的拉力分别为T1、T2，且T1与T2之比为5∶7。钢丝绳的重、滑轮与轴的摩擦及水对物体的阻力均忽略不计。（g取10N/kg）

求：（1）物体的重力G；
（2）物体浸没在水中匀速上升的过程中，滑轮组AB的机械效率η；
（3）物体全部露出水面后匀速上升的速度v物。

某科技小组设计从水中打捞重物A的装置如图所示，小文站在地面上通过滑轮组从水中提升重为1200N的物体A。当物体A在水面下，小文以拉力F₁匀速竖直拉动绳子，滑轮组的机械效率为η₁，小文对地面的压力为N₁；当物体A完全离开水面，小文以拉力F₂匀速竖直拉动绳子，滑轮组的机械效率为η₂，小文对地面的压力为N₂。已知：物体A的密度为3×10³kg/m³，小文的重力为600N，N₁: N₂=7:5。不计绳的质量和滑轮与轴之间的摩擦，g取10N/kg。求：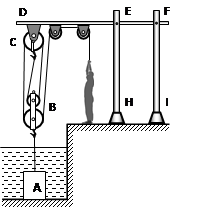

(1)物体在水面下受到的浮力；
(2)动滑轮受到的重力
(3)η₁与η₂的比值。

如图所示，滑轮下挂重500N的物体G，滑轮重40N，绳和杠杆都是轻质的。要在图示位置使杠杆平衡，（杠杆上标度的间距相等）

求： （1）滑轮绳子自由端拉力是多大？  
（2）在杠杆的A点所加的竖起向上的力F应是多大？

小明做俯卧撑时（如图23所示），可将其视为一个杠杆，重心在O点。他将身体撑起时，地面对两脚尖的支持力为250N，两脚尖与地面的接触面积为60cm²，双手与地面的接触面积为300cm²。

⑴画出以B为支点时重力的力臂L。
⑵如果小明的两脚尖对地面的压强与双手对地面的压强之比为5∶2，地面对双手的支持力为多少？
⑶小明在1min内做了30个俯卧撑，每次肩部上升的距离都为0.36m，则他1min内克服重力所做的功为多少?

如图所示，质量为8kg，边长为5cm的正方体物块A置于水平地面上，通过细绳系于轻质杠杆BOC的B端，杠杆可绕O点转动，且CO=3BO，在C端用F=20N的力竖直向下拉杠杆，使杠杆在水平位置平衡．（绳重不计，g取10N/kg）

求：（1）物体A的重力G；
（2）B端细绳的拉力F_拉；
（3）物体A对地面的压力F_压；
（4）物体A对地面的压强P．

杆秤是用来测量物体质量的工具，也是我国劳动人民智慧的结晶。如图所示，杆秤的提纽到挂钩的距离OA＝4cm，当秤砣移动到离提纽的距离为20cm时，杆秤刚好水平平衡，若秤砣的质量为0.6kg，求：

（1）所称物体的质量是多少kg？
（2）若用质量为0.5kg的秤砣去测量该物体，当杆秤刚好水平平衡时秤砣移动到离提纽的距离为多少cm？

如图所示轻质杠杆，把密度均为4.0×103kg/m3的甲、乙两个实心物体挂在A、B两端时，杠杆在水平位置平衡，若将甲物体浸没在水中，同时把支点从O移到O′时，杠杆又在新的位置平衡，若两次支点的距离O O′为OA的，求：甲、乙两个物体的质量之比．

如图所示，轻质杠杆AD用两根软绳悬挂于天花板上，两绳分别系在杠杆上的B、C两点。已知杠杆的长度为0.8m，BC间的距离为0.2m，CD间的距离为0.2m。用细绳将滑轮组固定在杠杆的A端，物体E（其质量可变）挂在动滑轮的挂钩上，每个滑轮重均为60N。物体H通过细绳挂在杠杆的D端，其质量始终保持不变。为使杠杆AD保持水平平衡，滑轮组所能提升重物E的最大质量m₁与最小质量m₂之比为4:1。杠杆、细绳的质量及一切摩擦均可忽略不计，取g= 10N/kg。求：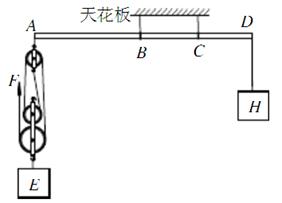

（1）滑轮组对杠杆A端的最大拉力F_A1与最小拉力F_A2之比；
（2）重物E的最大质量m₁；
（3）滑轮组的最小机械效率。（百分号前保留整数）

如图是一个上肢力量健身器示意图．D是动滑轮；配重A的底面积为5×10^﹣2m2，放在水平地面上对地面的压强P₀为2.4×10⁴Pa．杠杆EH可绕O点在竖直平面内转动，OE：OH=2：5．此人受到的重力为600N，他通过细绳在H点施加竖直向下的拉力T₁时，杠杆在水平位置平衡，他对地面的压力为F₁，配重A对地面的压力为F_A1，配重A受到的拉力为T_A1．配重A对地面的压强P₁为6×10³Pa；他在H点施加竖直向下的拉力T₂时，杠杆仍在水平位置平衡，他对地面的压力为F₂，配重A对地面的压力为F_A2，配重A受到的拉力为T_A2，配重A对地面的压强P₂为4×10³Pa．已知F₁：F₂=20：19，杠杆EH和细绳的质量均忽略不计．求：

（1）配重A受到的重力G_A．
（2）拉力T_A1和T_A2．
（3）动滑轮D受到的重力G_D．

为了监测水库的水位，小明设计了利用电子秤显示水库水位的装置。该装置由长方体A和B、滑轮组、轻质杠杆CD、电子秤等组成，且杠杠始终在水平位置平衡，OC:OD=1:2，如图所示。

已知A的体积为0.03m³，A所受的重力600N,B所受的重力为110N；当水位上涨到与A的上表面相平时，水面到水库底部的距离h=20m。不计滑轮和绳的重力与摩擦。已知水的密度为1x10³kg/m³.求：
(l）水库底部受到水的压强；
(2)A受到的浮力；
(3）此时电子秤受到B对它的压力。

俯卧撑是一项常见的体育健身运动。如图所示是李华同学做俯卧撑时的示意图。已知李华体重600N，1min钟内做了30个，每做一次肩膀升高40cm，李华身体可视为杠杆，O点为支点，A′点为重心，OA＝1m，B点到O点的距离OB＝1.5m.求：

（1）地面对手的支持力F；
（2）若每个手掌的面积是0.02m²，求双手对地面的压强是10⁴Pa；
（3）1min钟内李华所做的功是4800J；
（4）李华做功的功率P。

如图甲所示，底面积为50cm²的圆柱形玻璃筒中装有一定量的水，放在水平台面上，底面积为10cm²的圆柱形物体B浸没在水中，杠杆CD可绕支点O在竖直平面内转动，CO＝2DO；物体A是质量为100g的配重物。
在物体A上再加一个0.6N的向下拉力F，杠杆会转动到在水平位置平衡，如图乙所示，此时物体B有2/5的体积露出水面，筒中水的深度比图甲中水的深度下降了0.4cm。
（取10N/kg，杠杆、悬挂物体的细绳的质量均忽略计）

求：（1）物体B的体积；
（2）乙图中物体B所受的浮力大小；
（3）乙图中物体B底部所受水的压强大小；
（4）物体B的密度。

图是液压汽车起重机从水中打捞重物的示意图。A是动滑轮，B是定滑轮，C是卷扬机，D是油缸，E是柱塞。卷扬机转动使钢丝绳带动动滑轮上升，同时提升重物。被打捞的重物体积是，若在本次打捞前，起重机对地面的压强 p₀＝2.0×10⁷Pa，当物体在水中匀速上升时起重机对地面的压强p₁＝2.375×10⁷Pa，物体全部出水面后起重机对地面的压强p₂＝2.5×10⁷Pa，假设起重时柱塞沿竖直方向，物体出水前、后柱塞对吊臂的支撑力分别为N₁和N₂，N₁与N₂之比为19：24。重物出水后上升的速度，吊臂、定滑轮、钢丝绳的重以及轮与绳的摩擦不计。（g取10N/kg）求：

（1）被打捞物体的密度；
（2）若被打捞物体在水中匀速上升时滑轮组AB 的机械效率为，物体全部露出水面在空气中匀速上升时，滑轮组AB 的机械效率为，求 
（3）重物出水后，卷扬机牵引力的功率。

图是液压汽车起重机从水中打捞重物的示意图。C是卷扬机，E是液压机的柱塞，能够竖直向上支撑起重臂OMB。在起重臂的两端分别固定有定滑轮，图中虚线框内是悬挂在起重臂B端的滑轮组（未画完整，其中A是定滑轮），卷扬机经O点和B点的定滑轮拉动滑轮组的钢丝绳自由端K，使重物始终以恒定的速度匀速上升。当重物完全浸没在水中上升的过程中，地面对起重机的支持力N₁为1.225×10⁵N，柱塞E对起重臂的支撑力为F₁，卷扬机对钢丝绳自由端K的拉力T₁为6.25×10³N，滑轮组的机械效率为η；重物被完全拉出水面后上升的过程中，地面对起重机的支持力N₂为1.375×10⁵N，柱塞E对起重臂的支撑力为F₂，卷扬机的输出功率P₂为5kW，对钢丝绳自由端K的拉力为T₂。已知定滑轮A的质量m_A为200kg，虚线框内动滑轮的总质量m_D为250kg，F₁：F₂=9：14。若不计起重臂、钢丝绳的质量及滑轮组的摩擦，g取10N/kg，求：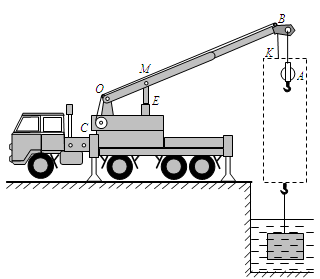

（1）被打捞的重物浸没在水中时受到的浮力F_浮；
（2）滑轮组的机械效率η；
（3）卷扬机拉动钢丝绳的速度v。