初中物理密度的计算计算题

如图所示，水平桌面上放置一圆柱形容器，其内底面积为 $200c{m}^2$，容器侧面靠近底部的位置有一个由阀门 $K$控制的出水口，物体 $A$是边长为 $10\mathit{cm}$的正方体，用不可伸长的轻质细线悬挂放入水中静止，此时有 $\frac{1}{5}$的体积露出水面，细线受到的拉力为 $12N$，容器中水深为 $18\mathit{cm}$。已知，细线能承受的最大拉力为 $15N$，细线断裂后物体 $A$下落过程不翻转，物体 $A$不吸水， $g$取 $10N/\mathit{kg}$。

（1）求物体 $A$的密度；

（2）打开阀门 $K$，使水缓慢流出，问放出大于多少 $\mathit{kg}$水时细线刚好断裂？

（3）细线断裂后立即关闭阀门 $K$，关闭阀门 $K$时水流损失不计，物体 $A$下落到容器底部稳定后，求水对容器底部的压强；

（4）从细线断裂到物体 $A$下落到容器底部的过程中，求重力对物体 $A$所做的功。

某物理兴趣小组设计了探测湖底未知属性的矿石密度的装置，其部分结构如图甲所示。电源电压为6V，R₀为定值电阻，滑动变阻器R的阻值随弹簧的拉力F变化关系如图乙，T为容器的阀门。某次探测时，水下机器人潜入100m深的湖底取出矿石样品M．返回实验室后，将矿石样品M悬挂于P点放入容器中，保持静止状态。打开阀门T，随着水缓慢注入容器，电压表示数U随容器中水的深度h变化关系如图丙中的实线所示。在电压表示数从2V变为4V的过程中，电流表示数变化值为0.2A（弹簧电阻忽略不计，矿石M不吸水，湖水密度与水相同，g＝10N/kg）。求：

（1）水下机器人在100m深的湖底取样时受到水的压强为多少？

（2）定值电阻R₀的阻值是多少？

（3）矿石M的密度是多少kg/m³？

某兴趣小组在实验室（温度为20℃）进行综合实验。装置如图所示，长为0.6m的绝缘轻质杠杆ab悬挂在高处，可绕O点转动。点O距杠杆b端0.2m。杠杆a端的轻质丝线悬挂一体积为2×10 ^{﹣ 3}m ³的实心合金块B，B浸没在烧杯内的液体中。已知该液体热胀冷缩的特性显著。其在温度为20℃时的密度为1.0×10 ³kg/m ³．当杠杆b端用轻质金属丝悬吊一质量为2kg的铜柱时，杠杆正好在水平位置平衡。此时，铜柱下的金属探针（重力不计）正好伸到水银槽的水银面上并且刚好和水银接触。右方电路中，小灯泡发光，导线C和金属丝良好接触但对金属丝和杠杆都不产生力的作用。导线A始终和槽中水银良好接触。已知小灯泡规格为"3V0.06W"，电源电压为3V．铜柱、探针、水银的电阻均不计。忽略温度对灯丝电阻的影响。求：

（1）若在电路中串联一个量程为0～15mA的电流表，为保证电路安全。定值电阻R的最小阻值是多少？

（2）合金块B的密度是多少？

（3）除烧杯内的液体外，装置中其他物体的热胀冷缩忽略不计。若实验室温度骤然升高，小灯泡将 　  　（选填"继续发光"或"熄灭"）。

底面积为100cm ²的平底圆柱形容器内装有适量的水，放置于水平桌面上。现将体积为500cm ³，重为3N的木块A轻放入容器内的水中，静止后水面的高度为8cm，如图甲所示，若将一重为6N的物体B用细绳系于A的下方，使其恰好浸没在水中，如图乙所示（水未溢出），不计绳重及其体积，求：

（1）图甲中木块A静止时浸入水中的体积；

（2）物体B的密度；

（3）图乙中水对容器底部的压强。

工人用图所示装置，打捞深井中的边长为30cm的正方体石料，石料的密度为3´10³kg/m³。装置的OC、DE、FG三根柱子固定在地面上，AB杆可绕O点转动，AO:OB=1:2，边长为L的正立方体配重M通过绳竖直拉着杆的B端。现用绳子系住石料并挂在滑轮的钩上，工人用力沿竖直方向向下拉绳，使石料以0.2m/s的速度从水中匀速提升。AB杆始终处于水平位置，绳子的质量、轮与轴间的摩擦均不计，g取10N/kg。求：

（1）如果石料在水中匀速上升时滑轮组的机械效率是η₁，石料完全离开水面后滑轮组的机械效率是η₂，且η₁：η₂=83:84，求石料在水中匀速上升过程中，工人拉绳的功率多大？
（2）若石料在水中匀速上升时，配重对地面的压强为6500帕，石料完全离开水面后，配重对地面的压强为4812.5帕；求配重M的密度。

阅读短文，回答文后的问题。

                                     体脂率

脂肪是人体的重要成分，主要分布在内脏周围和皮肤下面，脂肪供给维持生命必需的能量，氧化热值约为 $3.8\times {10}^{7}J/\mathit{kg}$，皮下脂肪还能防止热量散失，脂肪过量使人肥胖、并导致一些慢性疾病，人体脂肪率表示脂肪含量的多少、简称体脂率，是人体中脂肪质量与人体总质量的百分比，脂肪的密度约为 $0.9g/c{m}^3$、肌肉、骨骼等人体其他成分的精密度为 $1.1g/c{m}^3$，只要测出人体组织密度就可以算出体脂率，人体阻值密度可以采用水下称重法测量：先测出受试人的肺活量 $V$，然后用称量设备测出人的重力 $G_1$，受试人进入，浸没在水面下尽力呼气，此时体内剩余气体约为肺活量的 $\frac{1}{4}$，用称量设备测量体重的重力为 $G_2$，水的密度为 ${\rho }_{水}$．由此可以计算出人体阻值密度和体脂率，另外，因为脂肪几乎不含水分，其导电性和其他成分不同，所以还可以用测量人体电阻的办法来计算体脂肪率。

（1） $1\mathit{kg}$脂肪氧化最多可以释放的热量为　　 $J$。

（2）比较脂肪和人体其他成分的物理属性，下列说法错误的是　　。

$A$．密度较小    $B$．导热性较差 $C$．导电性较差   $D$．比热容较大

（3）人体组织密度的表达式为 ${\rho }_{人}=$　　（不用化简）。

（4）对过于肥胖无法自行浸没在水面下的人，可以采取什么措施进行水下称重？

如图甲所示，在容器底部固定一轻质弹簧，弹簧上端连有一边长为 $0.1m$的正方体物块 $A$，容器中水的深度为 $40\mathit{cm}$时，物块 $A$刚好完全浸没在水中。容器侧面的底部有一个由阀门 $B$控制的出水口，打开阀门 $B$，使水缓慢流出，当物块 $A$有 $\frac{2}{5}$的体积露出水面时，弹簧恰好处于自然伸长状态（即恢复原长没有发生形变），此时关闭阀门 $B$．弹簧受到的拉力 $F$跟弹簧的伸长量△ $L$关系如图乙所示。（已知 $g$取 $10N/\mathit{kg}$，水的密度为 ${\rho }_{水}=1.0\times {10}^3\mathit{kg}/m^3$，不计弹簧所受的浮力，物块 $A$不吸水）。求：

（1）打开阀门前物块 $A$受到的浮力；

（2）物块 $A$的密度；

（3）弹簧恰好处于自然伸长状态时水对容器底部压强。

水平桌面上有一底面积为 $5S_0$ 的圆柱形薄壁容器，容器内装有一定质量的水。将底面积为 $S_0$ 、高为 $h_0$ 的柱形杯装满水后（杯子材料质地均匀），竖直放入水中，静止后容器中水的深度为 $\frac{1}{2}{h}_0$ ，如图1所示；再将杯中的水全部倒入容器内，把空杯子竖直正立放入水中，待杯子自由静止后，杯底与容器底刚好接触，且杯子对容器底的压力为零，容器中水的深度为 $\frac{2}{3}{h}_0$ ，如图2所示。已知水的密度为 ${\rho }_0$ 。求：

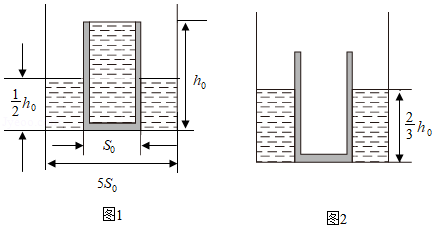
（1）空杯子的质量；

（2）该杯子材料的密度。

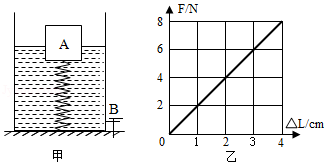
如图甲所示，一轻质弹簧，其两端分别固定在容器底部和正方体物块上。已知物块的边长为10cm，弹簧没有发生形变时的长度为15cm，弹簧受到拉力作用后，伸长的长度ΔL与拉力F的关系如图乙所示。向容器中加水，直到物块上表面与水面相平，此时水深30cm。

（1）该物块受到水的浮力；

（2）该物块的密度；

（3）打开出水口，缓慢放水，当弹簧恢复原状时，关闭出水口。求放水前后水对容器底部压强的变化量。

今年小明家种植柑橘获得了丰收。小明想：柑橘的密度是多少呢？于是，他将柑橘带到学校实验室，用天平、溢水杯来测量柑橘的密度。他用天平测出一个柑橘的质量是114g，又用溢水杯测出了一个柑橘的体积是120 cm³。小明测体积的方法是：先用天平称出装满水的溢水杯的总质量是360g，然后借助铅笔使这个柑橘浸没在溢水杯中，当溢水杯停止排水后再取出柑橘，接着测得溢水杯的总质量是240g，然后他算出了一个柑橘的体积V_橘＝V_排＝m_排／ρ_水＝120 g／1.0 g/cm³＝120 cm³ 。

请根据上述实验过程解答下列问题：
（1）溢水杯中排出水的质量是多大？浸没在水中的柑橘受到的浮力是多大？
（2）这个柑橘的密度是多大？
（3）小明用这种方法测出的这个柑橘的密度与它的实际密度比较，是偏大还是偏小？为什么？

目前国际上酒的度数表示法有三种，其中一种称为标准酒度，是指在温度为20℃的条件下，每100毫升酒液中所含酒精量的毫升数，中国也使用这种表示法，它是法国著名化学家盖·吕萨克制定的，又称盖·吕萨克酒度．蒸馏出来的酒液需要进行勾兑，勾兑一方面为了保障酒的品质，另一方面可以调整酒的度数，若现有60度和30度的酒液各若干，酒液中的微量元素忽略不计，求：
(1) 60度酒液的密度；
(2)如果用这两种酒液进行勾兑，获得42度、1000 ml的酒液，那么需要这两种酒液各多少毫升。
（已知ρ_酒精＝0.8×l0³ kg/m³，ρ_水＝1.0×10³ kg/m³，不考试酒液混合后体积减小）

某物理兴趣小组设计了探测湖底未知属性的矿石密度的装置，其部分结构如图甲所示。电源电压为6V，R₀为定值电阻，滑动变阻器R的阻值随弹簧的拉力F变化关系如图乙，T为容器的阀门。某次探测时，水下机器人潜入100m深的湖底取出矿石样品M．返回实验室后，将矿石样品M悬挂于P点放入容器中，保持静止状态。打开阀门T，随着水缓慢注入容器，电压表示数U随容器中水的深度h变化关系如图丙中的实线所示。在电压表示数从2V变为4V的过程中，电流表示数变化值为0.2A（弹簧电阻忽略不计，矿石M不吸水，湖水密度与水相同，g＝10N/kg）。求：

（1）水下机器人在100m深的湖底取样时受到水的压强为多少？

（2）定值电阻R₀的阻值是多少？

（3）矿石M的密度是多少kg/m³？

如图是利用电子秤监控水库水位的模拟装置，由长方体A和B、滑轮组、轻质杠杆CD、电子秤等组成。杠杆始终在水平位置平衡。已知OC：OD＝1：2，A的体积为0.02m ³，A重为400N，B重为150N，动滑轮重100N，不计绳重与摩擦（ρ _水＝1.0×10 ³kg/m ³）。求：

（1）A的密度；

（2）单独使用该滑轮组在空气中匀速提升A时的机械效率；

（3）水位上涨到A的上表面时，A受到的浮力；

（4）水位上涨过程中，电子秤所受的最大压力。

已知一根质量分布均匀的圆柱体木料质量为 $60\mathit{kg}$ ，体积为 $0.1m^3$ 。问：

（1）此木料的密度为多少？

（2）如图所示，甲、乙两人分别在 $A$ 点和 $B$ 点共同扛起此木料并恰好水平，其中 $\mathit{AO}=\mathit{BO}$ ， $O$ 为木料的中点。求此时乙对木料的作用力大小。

（3）若在（2）中当乙的作用点从 $B$ 点向 $O$ 点靠近时，请列式分析此过程中甲对木料作用力大小变化情况。

如图所示是一个水位监测仪的简化模型。杠杆 $\mathit{AB}$ 质量不计， $A$ 端悬挂着物体 $M$ ， $B$ 端悬挂着物体 $N$ ，支点为 $O$ ， $\mathit{BO}=4\mathit{AO}$ 。物体 $M$ 下面是一个压力传感器，物体 $N$ 是一个质量分布均匀的实心圆柱体，放在水槽中，当水槽中无水时，物体 $N$ 下端与水槽的底部恰好接触且压力为零，此时压力传感器的示数也为零。已知物体 $N$ 的质量 $m_2=4\mathit{kg}$ ，高度 $H=1m$ ，横截面积 $S=20c{m}^2(g$ 取 $10N/\mathit{kg}$ ， ${\rho }_{水}=1.0\times {10}^3\mathit{kg}/m^3)$ 。求：

（1）物体 $N$ 的密度 $\rho$ ；

（2）物体 $M$ 的质量 $m_1$ ；

（3）当压力传感器的示数 $F=40N$ 时，求水槽内水的深度 $h$ 。