如图, ,过点 作 且 ,得 ;再过点 作 且 ,得 ;又过 作 且 ,得 ,依此法继续下去,得 _____.

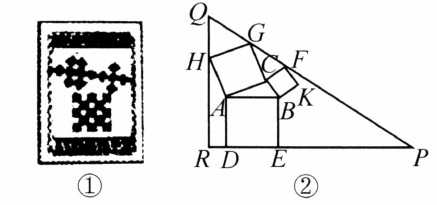
勾股定理有着悠久的历史,它曾引起很多人的兴趣.1955年希腊发行了一枚以勾股图为背景的邮票(如图①.所谓勾股图是指以直角三角形的三边为边向外作正方形构成的图形。它可以验证勾股定理.在图②的勾股图中,已知 .作 使得 ,点 在边 上,点 在边 上,点 在边 上,那么 的周长等于_____.
已知三角形相邻两边长分别为 和 ,第三边上的高为 ,则此三角形的面积为_____ .
如图,一只小猫沿着斜立在墙角的木板往上爬,木板底端距离墙角 ,当小猫从木板底端爬到顶端时,木板底端向左滑动了 ,木板顶端向下滑了 ,则小猫在木板上爬动了_____ .

如图是一种“羊头”形图案。其作法是:从正方形①开始,以它的一边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形②和②’,…,依此类推,若正方形①的边长为 ,则正方形⑦的边长为_____ .

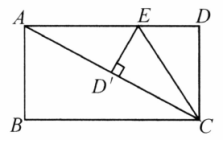
如图,将长方形纸片 折叠,使边 落在对角线 上,折痕为 ,且 点落在对角线 处.若 ,则 的长为_____.
已知 为有理数, 分别表示 的整数部分和小数部分,且 1,则 _____.