如图有一座抛物线形拱桥,桥下面在正常水位是AB宽20m,水位上升3m就达到警戒线CD,这是水面宽度为10m。(1)在如图的坐标系中求抛物线的解析式。(2)若洪水到来时,水位以每小时0.2m的速度上升,从警戒线开始,再持续多少小时才能到拱桥顶?
|

某地震救援队探测出某建筑物废墟下方点 C 处有生命迹象,已知废墟一侧地面上两探
测点A、B 相距 3 米,探测线与地面的夹角分别是30°和 60°(如图),试确定生命
所在点 C 的深度.(结果精确到0.1米,参考数据: )
)
如图,AC是某市环城路的一段,AE,BF,CD都是南北方向的街道,其与环城路AC的交
叉路口分别是A,B,C.经测量花卉世界D位于点A的北偏东45°方向、点B的北偏东
30°方向上,AB=2km,∠DAC=15°。
(1)求B、D之间的距离;
(2)求C、D之间的距离。 
已知:如图一次函数y= x+1的图象与x轴交于点A,与y轴交于点B;二次函数y=
x+1的图象与x轴交于点A,与y轴交于点B;二次函数y= x2+bx+c的图象与一次函数y=
x2+bx+c的图象与一次函数y= x+1的图象交于B、C两点,与x轴交于D、E两点且D点坐标为(1,0)
x+1的图象交于B、C两点,与x轴交于D、E两点且D点坐标为(1,0)
(1)求二次函数的解析式;
(2)求四边形BDEC的面积S;
(3)在x轴上是否存在点P,使得△PBC是以P为直角顶点的直角三角形?若存在,求出所有的点P,若不存在,请说明理由.
(本小题6分)
有下面3个结论: ①存在两个不同的无理数, 它们的积是整数;②存在两个不同的无理数, 它们的差是整数;③存在两个不同的非整数的有理数, 它们的和与商都是整数. 先判断这3个结论分别是正确还是错误的, 如果正确, 请举出符合结论的两个数.
(本小题12分)
如图, 中,
中,
 ,
, .它的顶点
.它的顶点 的坐标为
的坐标为 ,顶点
,顶点 的坐标为
的坐标为 ,点
,点 从点
从点 出发,沿
出发,沿 的方向匀速运动,同时点
的方向匀速运动,同时点 从点
从点 出发,沿
出发,沿 轴正方向以相同速度运动,当点
轴正方向以相同速度运动,当点 到达点
到达点 时,两点同时停止运动,设运动的时间为
时,两点同时停止运动,设运动的时间为 秒.
秒.
(1)求 的度数.(直接写出结果)
的度数.(直接写出结果)
(2)当点 在
在 上运动时,
上运动时, 的面积
的面积 与时间
与时间 (秒)之间的函数图象为抛物线的一部分(如图),求点
(秒)之间的函数图象为抛物线的一部分(如图),求点 的运动速度.
的运动速度.
(3)求题(2)中面积 与时间
与时间 之间的函数关系式,及面积
之间的函数关系式,及面积 取最大值时点
取最大值时点 的坐标.
的坐标.
(4)如果点 保持题(2)中的速度不变,当t取何值时,PO=PQ,请说明理由.
保持题(2)中的速度不变,当t取何值时,PO=PQ,请说明理由.
某环保小组为了解世博园的游客在园区内购买瓶装饮料数量的情况,一天,他们分别在A、B、C三个出口处,对离开园区的游客进行调查,其中在A出口调查所得的数据整理后绘成图
(1)在A出口的被调查游客中,购买2瓶及2瓶以上饮料的游客人数占A出口的被调查游客人数的______%.
(2)试问A出口的被调查游客在园区内人均购买了多少瓶饮料?
(3)已知B、C两个出口的被调查游客在园区内人均购买饮料的数量如表一所示若C出口的被调查人数比B出口的被调查人数多2万,且B、C两个出口的被调查游客在园区
内共购买了49万瓶饮料,试问B出口的被调查游客人数为多少万?
| 出 口 |
B |
C |
| 人均购买饮料数量(瓶) |
3 |
2 |
已知反比例函数y= (m为常数)的图象经过点A(-1,6).
(m为常数)的图象经过点A(-1,6).
(1)求m的值;
(2)如图,过点A作直线AC与函数y= 的图象交于点B,与x轴交于点C,且AB=2BC,求点C的坐标.
的图象交于点B,与x轴交于点C,且AB=2BC,求点C的坐标.
(每小题7分,共14分)
(1)计算:︱—2︱—(1+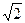 )0+
)0+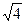 ;
; x+3>0
x+3>0
(2)解不等式组:
3(x-1)≤2x-1
(8分) 如图,有两个 的网格,网格中每个小正方形的边长均为1,每个网格中各画有一个梯形.请在图1、图2中分别画出一条线段,同时满足以下要求:
的网格,网格中每个小正方形的边长均为1,每个网格中各画有一个梯形.请在图1、图2中分别画出一条线段,同时满足以下要求:
(1)线段的一个端点为梯形的顶点,另一个端点在梯形一边的格点上;
(2)将梯形分成两个图形,其中一个是轴对称图形;
(3)图1、图2中分成的轴对称图形不全等.
(10分)康乐公司在 两地分别有同型号的机器
两地分别有同型号的机器 台和
台和 台,现要运往甲地
台,现要运往甲地 台,乙地
台,乙地 台,从
台,从 两地运往甲、乙两地的费用如下表:
两地运往甲、乙两地的费用如下表:
| |
甲地(元/台) |
乙地(元/台) |
| 地 |
 |
 |
| 地 |
 |
 |
(1)如果从地运往甲地 台,求完成以上调运所需总费用
台,求完成以上调运所需总费用 (元)与
(元)与 (台)之间的函数关系式;
(台)之间的函数关系式;
(2)请你为康乐公司设计一种最佳调运方案,使总费用最少,并说明理由。
(本题4分)
把下列各数填在相应的大括号里: ,
, ,0.86,
,0.86, ,
, ,0,
,0,

负整数集合:( …);
负分数集合:( …);
正分数集合:( …);
非负有理数集合( …)。
(本题6分)已知 、
、 互为相反数且
互为相反数且 ,
, 、
、 互为倒数,
互为倒数, 的绝对值是最小的正整数,求
的绝对值是最小的正整数,求 的值
的值