已知△ABC在平面直角坐标系中的位置如图所示.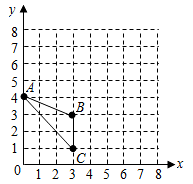
(1)分别写出图中点A和点C的坐标;
(2)画出△ABC绕点C按顺时针方向旋转90°后的△A′B′C′;
(3)求点A旋转到点A′所经过的路线长(结果保留π)
如图,在菱形ABCD中,AB=2, ,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.
,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.
(1)求证:四边形AMDN是平行四边形;
(2)填空:①当AM的值为 时,四边形AMDN是矩形;
②当AM的值为 时,四边形AMDN是菱形。
如图,△ABC和△AED是等腰直角三角形,∠BAC=∠EAD=90°,点D、E在∠BAC的外部,连结DC,BE.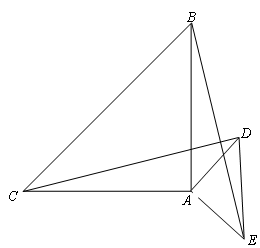
(1)求证:BE=CD;
(2)若将△AED绕点A旋转,直线CD交直线AB于点G,交直线BE于点K.
①如果AC=8,GA=2,求GC·KG的值;
②当△BED为等腰直角三角形时,请你直接写出AB∶BD的值.
如图,A、D、F、B在同一直线上,AE=BC,且AE∥BC,AD=BF.
(1)求证: ;
;
(2)连ED,CF,则四边形EDCF是 .(从平行四边形,矩形,菱形,正方形中选填).
南通百货大搂服装柜在销售中发现:“宝乐”牌童装平均每天可售出20件,每件盈利40元.元旦将至,商场决定采取适当的降价措施,扩大销售量,增加盈利,尽快减少库存.经市场调查发现:如果每件童装降价1元,那么平均每天就可多售出2件.要想平均每天销售这种童装盈利1200元,那么每件童装应降价多少元?
如图,在扇形OAB中,∠AOB=90°,半径OA=6.将扇形OAB沿过点B的直线折叠。点O恰好落在弧AB上点D处,折痕交OA于点C,求整个阴影部分的周长和面积。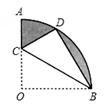
【改编】如图,直线a,b相交,∠2比∠1的3倍还大20°,求∠2、∠3、∠4的度数.
如图,已知点A(-4,8)和点B(2,n)在抛物线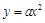 上.求a的值及点B的坐标.
上.求a的值及点B的坐标. 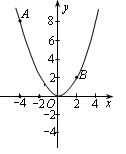
如图是根据某班40名同学一周的体育锻炼情况绘制的条形统计图,那么该班40名同学一周体育锻炼时间的众数、中位数分别是
| A.16,10.5 | B.8,9 | C.16,8.5 | D.8,8.5 |
(本题满分12分, 第(1)小题4分,第(2)小题4分,第(3)小题4分)
如图,已知等腰梯形ABCD中,AD∥BC,AD=1,BC=3,AB=CD=2,点E在BC边上,AE与BD交于点F,∠BAE=∠DBC,
(1)求证:△ABE∽△BCD;
(2)求tan∠DBC的值;
(3)求线段BF的长.