初中数学选择题

如图，已知二次函数与一次函数 的图像相交于点A（-3,5），B（7，2），则能使 成立的x的取值范围是（    ）

A．

B．

C．

D．

如图，□ABCD的面积为20，点E，F，G为对角线AC的四等分点，连接BE并延长交AD于H，连接HF并延长交BC于点M，则△BHM的面积为（   ）

A．10

B．

C．4

D．5

如图所示的几何体是由一些小正方体组合而成的，则这个几何体的俯视图是(    )．

如图所示，把同样大小的黑色棋子摆放在正多边形的边上，按照这样的规律摆下去，则第个图形需要黑色棋子的个数是     ．

如图，图1是一个底面为正方形的直棱柱，现将图1切割成图2的几何体，则图2的俯视图是

如图，在平面直角坐标系中，A(1,0)，B(0,3)，以AB为边在第一象限作正方形ABCD,点D在双曲线y=(k≠0)上，将正方形沿x轴负方向平移 m个单位长度后，点C恰好落在双曲线上，则m的值是                      （   ）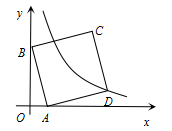

A．2

B．3

C．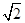

D．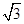

如图，将矩形纸片ABCD的四个角向内折起，恰好拼成一个无缝隙无重叠的四边形EFGH，若EH=3，EF=4，则边AD的长是（）

A．2

B．3

C．4．8

D．5

如图1，在平面直角坐标系中，将□ABCD放置在第一象限，且AB∥x轴．直线y=－x从原点出发沿x轴正方向平移，在平移过程中直线被平行四边形截得的线段长度l与直线在x轴上平移的距离m的函数图象如图2所示，那么ABCD面积为（   ）

A．4

B．4

C．8

D．8

如图，一圆柱高8 cm，底面半径为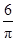 cm，一只蚂蚁从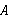点爬到点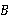处吃食，要爬行的最短路程是（    ）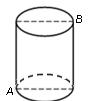

A．6 cm

B．8 cm

C．10 cm

D．12 cm

如图，正方形ABCD的对角线相交于O，点F在AD上，AD=3AF， △AOF的外接圆交AB于E，则的值为：（  ）

A．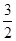

B．3

C．

D．2

在平面坐标系中，正方形ABCD的位置如图所示，点A的坐标为（1，0），点D的坐标为（0，2），延长CB交x轴于点A₁，作正方形A₁B₁C₁C，延长C₁B₁交x轴于点A₂，作正方形A₂B₂C₂C₁,……… 按这样的规律进行下去，第2012个正方形的面积为（   ）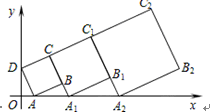

A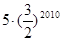．	B．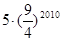
C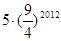．	D．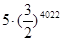

如图,在圆心角为90°的扇形MNK中，动点P从点M出发，沿运动，最后回到点M的位置。设点P运动的路程为x，P与M两点之间的距离为y，其图象可能是（ ）。

已知，+=0，则 =（    ）．   

A．1

B．-2013

C．-1

D．2013

在平面直角坐标系中，孔明做走棋游戏，其走法是；棋子从原点起，第1步向右走1个单位，第2步向右走2个单位，第3步向上走1个单位，第4步向右走1个单位，……依此类推，第n步是：当n能被3整除时，则向上走1个单位；当n被3除，余数是1时，则向右走1个单位，当n被3除，余数为2时，则向右走2个单位，当他走完第100步时，棋子所处位置的坐标是(　　)

A．(66，34)

B．(67，33)

C．(100，33)

D．(99，34)

定义：直线l₁与l₂相交于点O，对于平面内任意一点M，点M到直线l₁、l₂的距离分别为p、q，则称有序实数对(p，q)是点M的“距离坐标”．根据上述定义，“距离坐标”是(1，2)的个数是(　　)

A．2

B．3

C．4

D．5