△ABC中,∠C=90°,点D在边AB上,AD=AC=7,BD= BC.动点M从点C出发,以每秒1个单位的速度沿CA向点A运动,同时,动点N从点D出发,以每秒2个单位的速度沿DA向点A运动.当一个点到达点A时,点M、N两点同时停止运动.设M、N运动的时间为t秒.
BC.动点M从点C出发,以每秒1个单位的速度沿CA向点A运动,同时,动点N从点D出发,以每秒2个单位的速度沿DA向点A运动.当一个点到达点A时,点M、N两点同时停止运动.设M、N运动的时间为t秒.
⑴ 求cosA的值.
⑵ 当以MN为直径的圆与△ABC一边相切时,求t的值.
在直角坐标系中,A(0,4),B(4 ,0).点C从点B出发沿BA方向以每秒2个单位的速度向点A匀速运动,同时点D从点A出发沿AO方向以每秒1个单位的速度向点O匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点C、D运动的时间是t秒(t>0).过点C作CE⊥BO于点E,连结CD、DE.
,0).点C从点B出发沿BA方向以每秒2个单位的速度向点A匀速运动,同时点D从点A出发沿AO方向以每秒1个单位的速度向点O匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点C、D运动的时间是t秒(t>0).过点C作CE⊥BO于点E,连结CD、DE.
⑴ 当t为何值时,线段CD的长为4;
⑵ 当线段DE与以点O为圆心,半径为 的⊙O有两个公共交点时,求t的取值范围;
的⊙O有两个公共交点时,求t的取值范围;
⑶ 当t为何值时,以C为圆心、CB为半径的⊙C与⑵中的⊙O相切?
如图,直线y=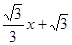 与x轴交于点A,与y轴交于点C,以AC为直径作⊙M,点
与x轴交于点A,与y轴交于点C,以AC为直径作⊙M,点 是劣弧AO上一动点(
是劣弧AO上一动点( 点与
点与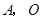 不重合).抛物线y=-
不重合).抛物线y=-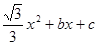 经过点A、C,与x轴交于另一点B,
经过点A、C,与x轴交于另一点B,
(1)求抛物线的解析式及点B的坐标;
(2)在抛物线的对称轴上是否存在一点P,是︱PA—PC︱的值最大;若存在,求出点P的坐标;若不存在,请说明理由。
(3)连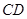 交
交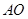 于点
于点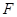 ,延长
,延长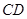 至
至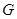 ,使
,使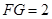 ,试探究当点
,试探究当点 运动到何处时,直线
运动到何处时,直线 与⊙M相切,并请说明理由.
与⊙M相切,并请说明理由.
如图:在等腰△ABC中,AB=AC,AD上BC,垂足为D,以AD为直径作⊙0,⊙0分别交AB、AC于E、F.
(1)求证:BE=CF;
(2)设AD、EF相交于G,若EF=8,BC=10,求⊙0的半径.
如图,在平面直角坐标系中,O为坐标原点,点A的坐标为(0,4),点B的坐标为(4,0),点C的坐标为(-4,0),点P在射线AB上运动,连结CP与y轴交于点D,连结BD.过P,D,B三点作⊙Q与y轴的另一个交点为E,延长DQ交⊙Q于点F,连结EF,BF.
(1)求直线AB的函数解析式;
(2)当点P在线段AB(不包括A,B两点)上时.
①求证:∠BDE=∠ADP;
②设DE=x,DF=y.请求出y关于x的函数解析式;
(3)请你探究:点P在运动过程中,是否存在以B,D,F为顶点的直角三角形,满足两条直角边之比为2:1?如果存在,求出此时点P的坐标:如果不存在,请说明理由.
已知直线y=x+6交x轴于点A,交y轴于点C,经过A和原点O的抛物线y=ax2+bx(a<0)的顶点B在直线AC上.
(1)求抛物线的函数关系式;
(2)以B点为圆心,以AB为半径作⊙B,将⊙B沿x轴翻折得到⊙D,试判断直线AC与⊙D的位置关系,并说明理由;
(3)若E为⊙B优弧 上一动点,连结AE、OE,问在抛物线上是否存在一点M,使∠MOA︰∠AEO=2︰3,若存在,试求出点M的坐标;若不存在,试说明理由.
上一动点,连结AE、OE,问在抛物线上是否存在一点M,使∠MOA︰∠AEO=2︰3,若存在,试求出点M的坐标;若不存在,试说明理由.
如图①,②,在平面直角坐标系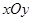 中,点
中,点 的坐标为(4,0),以点
的坐标为(4,0),以点 为圆心,4为半径的圆与
为圆心,4为半径的圆与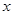 轴交于
轴交于 ,
, 两点,
两点, 为弦,
为弦, ,
, 是
是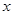 轴上的一动点,连结
轴上的一动点,连结 。
。
(1)求 的度数;
的度数;
(2)如图①,当 与⊙A相切时,求
与⊙A相切时,求 的长;
的长;
(3)如图②,当点 在直径
在直径 上时,
上时, 的延长线与⊙A相交于点
的延长线与⊙A相交于点 ,问
,问 为何值时,
为何值时, 是等腰三角形?
是等腰三角形?
如图,在平面直角坐标系xOy中,AB在x轴上,以AB为直径的半⊙O’与y轴正半轴交于点C,连接BC,AC.CD是半⊙O’的切线,AD⊥CD于点D.
(1)求证:∠CAD =∠CAB;
(2)已知抛物线 过A、B、C三点,AB=10,tan∠CAD=
过A、B、C三点,AB=10,tan∠CAD= .
.
① 求抛物线的解析式;
② 判断抛物线的顶点E是否在直线CD上,并说明理由;
③ 在抛物线上是否存在一点P,使四边形PBCA是直角梯形.若存在,直接写出点P的坐标(不写求解过程);若不存在,请说明理由.
如图1,在平面直角坐标系中,有一矩形ABCD,其三个顶点的坐标分别为A(2,0)、B(8,0)、C(8,3).将直线l:y=-3x-3以每秒3个单位的速度向右运动,设运动时间为t秒.

(1)当t=_________时,直线l经过点A.(直接填写答案)
(2)设直线l扫过矩形ABCD的面积为S,试求S>0时S与t的函数关系式.
(3)在第一象限有一半径为3、且与两坐标轴恰好都相切的⊙M,在直线l出发的同时,⊙M以每秒2个单位的速度向右运动,如图2所示,则当t为何值时,直线l与⊙M相切?
如图1,Rt△ABC两直角边的边长为AC=3,BC=4.
(1)如图2,⊙O与Rt△ABC的边AB相切于点X,与边BC相切于点Y.请你在图2中作出并标明⊙O的圆心(用尺规作图,保留作图痕迹,不写作法和证明)
(2)P是这个Rt△ABC上和其内部的动点,以P为圆心的⊙P与Rt△ABC的两条边相切.设⊙P的面积为S,你认为能否确定S的最大值?若能,请你求出S的最大值;若不能,请你说明不能确定S的最大值的理由.
如图1,在平面直角坐标系中,⊙O1与x轴切于A(-3,0)与y轴交于B、C两点,BC=8,连接AB。
(1)求证:∠ABO1=∠ABO;
(2)求AB的长;
(3)如图2,过A、B两点作⊙O2与y轴的正半轴交于M,与O1B的延长线交于N,当⊙O2的大小变化时,得出下列两个结论:①BM-BN的值不变;②BM+BN的值不变。其中有且只有一个结论正确,请判断①、②中哪个结论正确,并说明理由。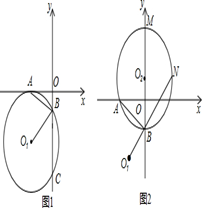
已知四边形ABCD是边长为4的正方形,以AB为直径在正方形内作半圆,P是半圆上的动点(不与点A、B重合),连接PA、PB、PC、PD.
(1)如图①,当PA的长度等于 时,∠PAB=60°;当PA的长度等于 时,△PAD是等腰三角形;
(2)如图②,以AB边所在直线为x轴、AD边所在直线为y轴,建立如图所示的直角坐标系(点A即为原点O),把△PAD、△PAB、△PBC的面积分别记为S1、S2、S3.坐标为(a,b),试求2 S1 S3-S22的最大值,并求出此时a,b的值.
如图,在直角体系中,直线AB交x轴于点A(5,0),交y轴于点B,AO是⊙M的直径,其半圆交AB于点C,且AC=3。取BO的中点D,连接CD、MD和OC。
(1)求证:CD是⊙M的切线;
(2)二次函数的图象经过点D、M、A,其对称轴上有一动点P,连接PD、PM,求△PDM的周长最小时点P的坐标;
(3)在(2)的条件下,当△PDM的周长最小时,抛物线上是否存在点Q,使 ?若存在,求出点Q的坐标;若不存在,请说明理由。
?若存在,求出点Q的坐标;若不存在,请说明理由。
如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为(4, ),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
(1)求抛物线的解析式及A,B两点的坐标;
(2)在(1)中抛物线的对称轴l上是否存在一点P,使AP+CP的值最小?若存在,求AP+CP的最小值,若不存在,请说明理由;
(3)在以AB为直径的⊙M相切于点E,CE交x轴于点D,求直线CE的解析式.
如图1,过点A(0,4)的圆的圆心坐标为C(2,0),B是第一象限圆弧上的一点,且BC⊥AC,抛物线 经过C、B两点,与x轴的另一交点为D。
经过C、B两点,与x轴的另一交点为D。
(1)点B的坐标为( , ),抛物线的表达式为 .
(2)如图2,求证:BD//AC;
(3)如图3,点Q为线段BC上一点,且AQ=5,直线AQ交⊙C于点P,求AP的长。