已知四边形ABCD是边长为4的正方形,以AB为直径在正方形内作半圆,P是半圆上的动点(不与点A、B重合),连接PA、PB、PC、PD.
(1)如图①,当PA的长度等于 时,∠PAB=60°;当PA的长度等于 时,△PAD是等腰三角形;
(2)如图②,以AB边所在直线为x轴、AD边所在直线为y轴,建立如图所示的直角坐标系(点A即为原点O),把△PAD、△PAB、△PBC的面积分别记为S1、S2、S3.坐标为(a,b),试求2 S1 S3-S22的最大值,并求出此时a,b的值.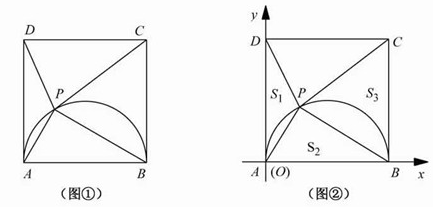
相关知识点
推荐套卷

 AF,AB=AC,EC与BF交于点O,∠A=600,∠B=250,求∠EOB的度数。
AF,AB=AC,EC与BF交于点O,∠A=600,∠B=250,求∠EOB的度数。
 。
。
 连结A B′。求证:△ABB′是等腰三角形。
连结A B′。求证:△ABB′是等腰三角形。
 粤公网安备 44130202000953号
粤公网安备 44130202000953号