如图1,在平面直角坐标系中,有一矩形ABCD,其三个顶点的坐标分别为A（2,0）、B（8,0）、C（8,3）．将直线l:y＝－3x－3以每秒3个单位的速度向右运动,设运动时间为t秒．
（1）当t＝_________时,直线l经过点A．（直接填写答案）
（2）设直线l扫过矩形ABCD的面积为S,试求S＞0时S与t的函数关系式．
（3）在第一象限有一半径为3、且与两坐标轴恰好都相切的⊙M,在直线l出发的同时,⊙M以每秒2个单位的速度向右运动,如图2所示,则当t为何值时,直线l与⊙M相切？
相关试题
如图，已知：D是△ABC中BC边上一点，EB=EC，∠ABE=∠ACE，求证：∠BAE=∠CAE.
证明：在△AEB和△AEC中，
∴△AEB≌△AEC(第一步)
∴∠BAE=∠CAE(第二步)
问：上面证明过程是否正确？若正确，请写出每一步推理根据；若不正确，请指出错在哪一步？并写出你认为正确的推理过程；
如图，在△ABC中，AB=CB，∠ABC=90°，D为AB延长线上一点，点E在BC上，且BE=BD，连结AE、DE、DC.
①求证：△ABE≌△CBD；
②若∠CAE=30°，求∠BDC的度数.
（4）
相关知识点
推荐套卷
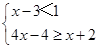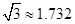粤公网安备 44130202000953号