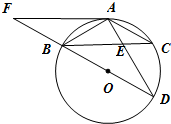
(8分)如图,AB是半圆的直径,点O是圆心,点C是OA的中点,CD⊥OA交
半圆于点D,点E是的中点,连接AE、OD,过点D作DP∥AE交BA的延长线于点P.
(1)求∠AOD的度数;
(2)求证:PD是半圆O的切线.
(本小题 10 分)如图,在 Rt△ABC中,∠ACB=90 D是AB 边上的一点,以BD为直径的⊙0与边 AC 相切于点E,连结DE并延长,与BC的延长线交于点 F .
D是AB 边上的一点,以BD为直径的⊙0与边 AC 相切于点E,连结DE并延长,与BC的延长线交于点 F .
( 1 )求证: BD =" BF" ;
( 2 )若 BC =" 12" , AD =" 8" ,求 BF 的长.
如图,等圆 和 相交于A、B两点,⊙
(1)求证:
是
的切线;
(2)求
的长。

如图,已知CD是⊙O的直径,AC⊥CD,垂足为C,弦DE∥OA,直线AE、CD
相交于点B.
(1)求证:直线AB是⊙O的切线.
(2)当AC=1,BE=2,求tan∠OAC的值.
(10分)如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于 点D,过
点D,过
点D作EF⊥AC于点E,交AB的延长线于点F.
(1)求证:EF是⊙O的切线;
(2)当∠B AC=60º时,DE与DF有何数量关系?请说明理由;
AC=60º时,DE与DF有何数量关系?请说明理由;
(3)当AB=5,BC=6时,求tan∠BAC的值.
.如图13,D为 O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是 O的切线;
O的切线;
(2)过点B作 O的切线交CD的延长线于点E,若BC=6,tan∠CDA=
O的切线交CD的延长线于点E,若BC=6,tan∠CDA= ,求BE的长
,求BE的长
(11·钦州)
如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D.
锐角∠DAB的平分线AC交⊙O于点C,作CD⊥AD,垂足为D,直线CD与AB的延长线交于点E.
(1)求证:AC平分∠DAB;
(2)过点O作线段AC的垂线OE,垂足为E(要求:尺规作图,保留作图痕迹,不写作法);
(3)若CD=4,AC=4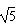 ,求垂线段OE的长.
,求垂线段OE的长.
(11·柳州)
如图,已知AB是⊙O的直径,锐角∠DAB的平分线AC交⊙O于点C,作CD⊥AD,垂足为D,直线CD与AB的延长线交于点E.
(1)求证:直线CD为⊙O的切线;
(2)当AB=2BE,且CE=时,求AD的长.
如图,已知⊙O的直径AB与弦CD互相垂直,垂足为点E. ⊙O的切线BF与
弦AD的延长线相交于点F,且AD=3,cos∠BCD=" " .
(1)求证:CD∥BF;
(2)求⊙O的半径;
(3)求弦CD的长. 
如图,D是△ABC的边BC的中点,过AD延长线上的点E作AD的垂线EF,E为垂足,EF与AB的延长线相交于点F,点O在AD上,AO=CO,BC∥EF.
(1)证明:AB=AC;
(2)证明:点O是△ABC的外接圆的圆心;
(3)当AB=5,BC=6时,连接BE,若∠ABE=90°,求AE的长.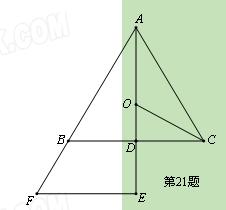
如图,某商标 是由边长均为2的正三角形、正方形、正六边形的金属薄片镶嵌而成的镶嵌图案.
是由边长均为2的正三角形、正方形、正六边形的金属薄片镶嵌而成的镶嵌图案.
(1)求这个镶嵌图案中一个正三角形的面积;
(2)如果在这个镶嵌图案中随机确定一个点O,那么点O落在镶嵌图案中的正方形区域的概率为多少?(结果保留二位小数)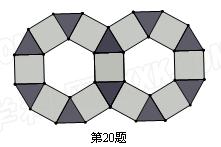
如图①,小慧同学把一个正三角形纸片(即△OAB)放在直线l1上,OA边与直线l1重合,然后将三角形纸片绕着顶点A按顺时针方向旋转120°,此时点O运动到了点O1处,点B运动到了点B1处;小慧又将三角形纸片AO1B1绕点B1按顺时针方向旋转120°,此时点A运动到了点A1处,点O1运动到了点O2处(即顶点O经过上述两次旋转到达O2处).
小慧还发现:三角形纸片在上述两次旋转的过程中,顶点O运动所形成的图形是两段
圆弧,即 和
和 ,顶点O所经过的路程是这两段圆弧的长度之和,并且这两段圆弧
,顶点O所经过的路程是这两段圆弧的长度之和,并且这两段圆弧
与直线l1围成的图形面积等于扇形AOO1的面积、△AO1B1的面积和扇形B1O1O2的面积之
和.
小慧进行类比研究:如图②,她把边长为1的正方形纸片OABC放在直线l2上,OA
边与直线l2重合,然后将正方形纸片绕着顶点^按顺时针方向旋转90°,此时点O运动到
了点O1处(即点B处),点C运动到了点C1处,点B运动到了点B1处;小慧又将正方形
纸片AO1C1B1绕顶点B1按顺时针方向旋转90°,……,按上述方法经过若干次旋转后.她
提出了如下问题:
问题①:若正方形纸片OABC接上述方法经过3次旋转,求顶点O经过的路程,并
求顶点O在此运动过程中所形成的图形与直线l2围成图形的面积;若正方形纸片OA BC
按上述方法经过5次旋转,求顶点O经过的路程;
问题②:正方形纸片OABC按上述方法经过多少次旋转,顶点O经过的路程是 ?
?
请你解答上述两个问题.
已知四边形ABCD是边长为4的正方形,以AB为直径在正方形内作半圆,P是半圆上的动点(不与点A、B重合),连接PA、PB、PC、PD.
(1)如图①,当PA的长度等于
时,∠PAB=60°;
当PA的长度等于 时,△PAD是等腰三角形;
(2)如图②,以AB边所在直线为x轴、AD边所在直线为y轴,建立如图所示的直角
坐标系(点A即为原点O),把△PAD、△PAB、△PBC的面积分别记为S1、S2、S3.坐
标为(a,b),试求2 S1 S3-S22的最大值,并求出此时a,b的值.
如图,已知AB是⊙O的 弦,OB=2,∠B=30°,
弦,OB=2,∠B=30°,
C是弦AB上的任意一点(不与点A、B重合),连接CO并延长CO交
于⊙O于点D,连接AD.
(1)弦长AB等于 ▲ (结果保留根号);
(2)当∠D=20°时,求∠BOD的度数;
(3)当AC的长度为多少时,以A、C、D为顶点的三角形与以B、
C、O为顶点的三角形相似?请写出解答过程.
如图,BD为⊙O的直径,AB=AC,AD交BC于点E,AE=2,ED=4,
(1)求证:△ABE∽△ADB;
(2)求AB的长;
(3)延长DB到F,使得BF=BO,连接FA,试判断直线FA与⊙O的位置关系,并说明理由.