(10分)如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于 点D,过
点D,过
点D作EF⊥AC于点E,交AB的延长线于点F.
(1)求证:EF是⊙O的切线;
(2)当∠B AC=60º时,DE与DF有何数量关系?请说明理由;
AC=60º时,DE与DF有何数量关系?请说明理由;
(3)当AB=5,BC=6时,求tan∠BAC的值.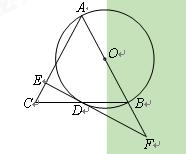
相关知识点
推荐套卷
(10分)如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于 点D,过
点D,过
点D作EF⊥AC于点E,交AB的延长线于点F.
(1)求证:EF是⊙O的切线;
(2)当∠B AC=60º时,DE与DF有何数量关系?请说明理由;
AC=60º时,DE与DF有何数量关系?请说明理由;
(3)当AB=5,BC=6时,求tan∠BAC的值.