如图,半圆O的直径AE=4,点B,C,D均在半圆上,若AB=BC,CD=DE,连接OB,OD,则图中阴影部分的面积是( )
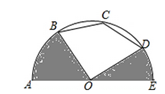
| A.π | B.2π | C.8 | D.11 |
如图,四边形ABCD为⊙O的内接四边形,已知∠BOD=100°,则∠BCD的度数为( )

| A.50° | B.80° | C.100° | D.130° |
如图所示,有一圆形展厅,在其圆形边缘上的点A处安装了一台监视器,它们监控角度是65°.为了监控整个展厅,最少需在圆形边缘上共安装这样的监视器( )台.
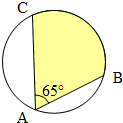
| A.2 | B.3 | C.4 | D.5 |
圆锥的母线长为4,底面半径为2,则此圆锥的侧面积是( )
| A.6π | B.8π | C.12π | D.16π |
如图,若AB是⊙O的直径,CD是⊙O的弦,∠ABD="58°" ,则∠BCD度数为( )
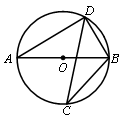
| A.116° | B.64° | C.58° | D.32° |
如图,△ABC的边AC与⊙O相交于C、D两点,且经过圆心O,边AB与⊙O相切,切点为B.已知∠A=30°,则∠C的大小是( )
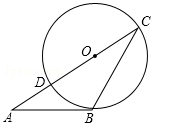
A.30° B.45° C.60° D.40°
点O是△ABC的外心,若∠BOC=80°,则∠BAC的度数为( )
| A.40° | B.100° | C.40°或140° | D.40°或100° |
如图,在Rt△ABC中∠ACB=90°,AC=6,AB=10,CD是斜边AB上的中线,以AC为直径作⊙O,设线段CD的中点为P,则点P与⊙O的位置关系是( )

| A.点P在⊙O内 | B.点P在⊙O上 |
| C.点P在⊙O外 | D.无法确定 |
如图,小明使一长为4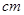 ,宽为3
,宽为3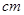 的长方形木板,在桌面上做无滑动的翻滚(顺时针方向)木板上点A位置变化为
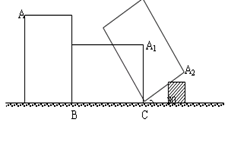
的长方形木板,在桌面上做无滑动的翻滚(顺时针方向)木板上点A位置变化为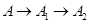 ,其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成30°角,则点A翻滚到A2位置时共走过的路径长为( )
,其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成30°角,则点A翻滚到A2位置时共走过的路径长为( )
A.10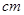 |
B.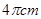 |
C.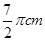 |
D.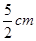 |
如图,A点是半圆上一个三等分点,B点是弧AN的中点,P点是直径MN上一动点,⊙O的半径为1,则AP+BP的最小值为( )
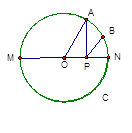
| A.1 | B.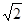 |
C.2 | D.无法计算 |
已知:关于x的一元二次方程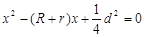 有两个相等的实数根,其中R 、r分别是⊙O
有两个相等的实数根,其中R 、r分别是⊙O 、 ⊙O
、 ⊙O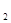 的半径,d为两圆的圆心距,则⊙O
的半径,d为两圆的圆心距,则⊙O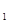 与⊙O
与⊙O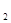 的位置关系是( ).
的位置关系是( ).
| A.外离 | B.外切 | C.相交 | D.内切 |
圆内接四边形ABCD中,∠A、∠B、∠C的度数比是2︰3︰6,则∠D的度数是( )
(A)67.5° (B)135° (C)112.5° (D)110°
在Rt△ABC中,∠C=90°,AC=12,BC=5,将△ABC绕边AC所在直线旋转一周得到圆锥,则该圆锥的侧面积是 ( )
| A.25π | B.65π | C.90π | D.130π |