初中数学圆幂定理选择题

如图，AB、AC是⊙O的两条弦，连结OB、OC．若∠BAC=60°，则∠BOC的度数（ ）

A．30°         B．60°          C．90°              D．120°

如图，AB是⊙O的直径，AB=8，点M在⊙O上，∠MAB=20°，N是弧MB的中点，P是直径AB上的一动点，若MN=1，则△PMN周长的最小值为（ ）．

A．4

B．5

C．6

D．7

已知圆锥的底面半径长为5，侧面展开后得到一个半圆，则该圆锥的母线长为（     ）

A．2．5

B．5

C．10

D．15

下列四个命题：（1）直径是弦；（2）经过三个点一定可以作圆；（3）平分弦的直径垂直于弦；（4）圆心角相等，所对的弧相等。其中正确的有（       ）

A． 1个

B． 2个

C．3个

D． 4

如图，在⊙O中，若C是的中点，则图中与相等的角还有（    ）

A．1个

B．3个

C．4个

D．5个

如图，圆心角∠BOC=78°，则圆周角∠BAC的度数是（    ）
 

A．156°

B．78°

C．39°

D．12°

如图，⊙O的半径是4，点P是弦AB延长线上的一点，连接OP，若OP=6，∠APO=30°，则弦AB的长为（   ）

A．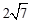

B．

C．5

D．

下列命题中的假命题是（   ）

A．正方形的半径等于正方形的边心距的倍

B．三角形任意两边的垂直平分线的交点是三角形的外心

C．用反证法证明命题“三角形中至少有一个内角不小于60°”时，第一步应该“假设每一个内角都小于60°”

D．过三点能且只能作一个圆

如图，A、B、P是⊙O上的三点，∠APB=40°，则弧AB的度数为（   ）

A．50°             B．80°           C．280°         D．80°或280°

下列说法中正确的是（   ）

A．平分弦的直径垂直于弦，并且平分弦所对的两条弧

B．圆是轴对称图形，每一条直径都是它的对称轴

C．弦的垂直平分线过圆心

D．相等的圆心角所对的弧也相等

如图，在Rt△ABC中，∠ABC=90°，AB=8cm，BC=6cm，分别以AC的长为半径作圆，将
Rt△ABC截去两个扇形，则余下阴影部分的面积为（    ）cm²

A．

B．24－

C．24－

D．24－

用一个圆心角为120°，半径为18cm 的扇形作一个圆锥的侧面，则这个圆锥的底面半径应等于（  ）

A．9cm

B．6cm

C．4cm

D．3cm

如图，在O中，直径CD⊥弦AB，则下列结论中正确的是（   ）

A．AD=AB

B．∠BOC=2∠D

C．∠D +∠BOC=90°

D．∠D=∠B

如图，AB是⊙O的一条弦，点C是⊙O上一动点，且AB=4，点分别是的中点，
直线与⊙O交于G、H两点，若⊙O的半径为5，当GE+FH的值最大时，弦BC的长等于（     ）
 

A．8

B．10

C．或8

D．或10

如图，四边形ABCD是⊙O的内接四边形，⊙O的半径为4，∠B=135°，则劣弧的长等于（  ）

A．

B．

C．

D．