初中数学圆幂定理试题

如图，点A、B、C分别是⊙O上的点，CD是⊙O的直径，P是CD延长线上的一点，AP=AC．

（1）若∠ABC=60°．求证：AP是⊙O的切线；
（2）若点B是弧CD的中点，AB交CD于点E，CD=4，求BE•AB的值．

如图OA=OB=OC且∠ACB=30°，则∠AOB＝       

 

如图，已知⊙O的直径AB与弦CD互相垂直，垂足为点E．⊙O的切线BF与弦AC的延长线相交于点F，且AC=8，tan∠BDC=．

（1）求⊙O的半径长；
（2）求线段CF长．

如图，⊙O的直径AC与弦BD相交于点F，点E是DB延长线上一点，∠EAB=∠ADB．

（1）求证：EA是⊙O的切线；
（2）已知点B是EF的中点，求证：以A、B、C为顶点的三角形与△AEF相似；
（3）已知AF=4，CF=2，在（2）的条件下，求AE的长．

小美和同学一起到游乐场游玩．游乐场的大型摩天轮的半径为20 m，匀速旋转1周需要12 min．小美乘坐最底部的车厢（离地面约0.5 m）开始1周的观光，请回答下列问题：（参考数据：≈1.414，≈1.732）

（1）1.5min后小美离地面的高度是   m；（精确到0.1m）
（2）摩天轮启动多长时间后，小美离地面的高度将首次达到10.5 m?
（3）摩天轮转动一周，小美在离地面10.5m以上的空中有多长时间？

如图，点A为⊙O上一个动点，点B在⊙O内，且OA=2，OB=2，当∠OAB的度数取最大值时，AB的长度为   ．

问题情境：如图1，P是⊙O外的一点，直线PO分别交⊙O于点A、B，则PA是点P到⊙O上的点的最短距离．

探究：
请您结合图2给予证明，
归纳：
圆外一点到圆上各点的最短距离是：这点到连接这点与圆心连线与圆交点之间的距离．
图中有圆，直接运用：
如图3，在Rt△ABC中，∠ACB=90°，AC=BC=2，以BC为直径的半圆交AB于D，P是上的一个动点，连接AP，则AP的最小值是       ．
        
图中无圆，构造运用：
如图4，在边长为2的菱形中，∠=60°，是边的中点，是边上一动点，将△沿所在的直线翻折得到△，连接,请求出长度的最小
值．

解：由折叠知，又M是AD的中点，可得，故点在以AD为直径的圆上．如图8，以点M为圆心，MA为半径画⊙M，过M作MH⊥CD，垂足为H，（请继续完成下列解题过程）
迁移拓展，深化运用：
如图6，E，F是正方形ABCD的边AD上两个动点，满足AE=DF．连接CF交BD于点G，连接BE交AG于点H．若正方形的边长为2，则线段DH长度的最小值是      ．

如图，AB为⊙O的直径，AB=30，正方形DEFG的四个顶点分别在半径OA、OC及⊙O上，且∠AOC=45°，则正方形DEFG的面积为         ．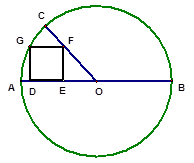

如图，正方形ABCD的对角线相交于O，点F在AD上，AD=3AF， △AOF的外接圆交AB于E，则的值为：（  ）

A．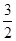

B．3

C．

D．2

（1）引入：如图1，直线AB为⊙O的弦，OC⊥OA,交AB于点P,且PC=BC，直线BC是否与⊙O相切，为什么？

（2）引申：记（1）中⊙O的切线为直线，在（1）的条件下，如图2，将切线向下平移，设平移后的直线与OB的延长线相交于点，与AB的延长线相交于点E，与OP的延长线相交于点．
找出图2中与相等的线段，并说明理由；
如果=9cm，=12cm，⊙O的半径为6cm，试求线段的长．

如图，平面直角坐标系xOy中，一次函数y=-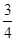x+b（b为常数，b＞0）的图象与x轴、y轴分别相交于点A、B，半径为4的⊙O与x轴正半轴相交于点C，与y轴相交于点D、E，点D在点E上方．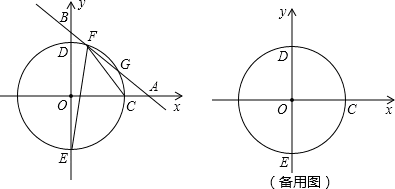

（1）若直线AB与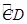有两个交点F、G．
①求∠CFE的度数；
②用含b的代数式表示FG²，并直接写出b的取值范围；
（2）设b≥5，在线段AB上是否存在点P，使∠CPE=45°？若存在，请求出P点坐标；若不存在，请说明理由．

如图，以矩形ABCD的对角线AC的中点O为圆心、OA长为半径作⊙O，⊙O经过B、D两点，过点B作BK⊥AC，垂足为K，过点D作DH∥KB，DH分别与AC、AB、⊙O及CB的延长线相交于点E、F、G、H。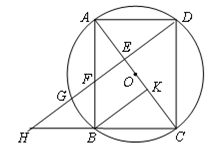

（1）求证：AE＝CK
（2）若AB＝a，AD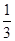＝a（a为常数），求BK的长（用含a的代数式表示）。
（3）若F是EG的中点，且DE＝6，求⊙O的半径和GH的长。

如图，AB为⊙O的直径，弦CD与AB相交于E，DE=EC，过点B的切线与AD的延长线交于F，过E作EG⊥BC于G，延长GE交AD于H．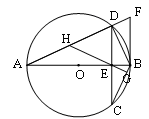

（1）求证：AH=HD；
（2）若AE:AD=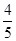，DF=9，求⊙O的半径。

．如图，BE是⊙O的直径，点A在EB的延长线上，弦PD⊥BE，垂足为C，连接OD，∠AOD=∠APC．

（1）求证：AP是⊙O的切线．
（2）若⊙O的半径是4，AP=4，求图中阴影部分的面积．

如图，已知平面直角坐标系中，⊙O的圆心在坐标原点，直线l与轴相交于点P，与⊙O相交于A、B两点，∠AOB=90°.点A和点B的横坐标是方程x²-x-k="0" 的两根，且两根之差为3.

（1）求方程x²-x-k="0" 的两根；
（2）求A、B两点的坐标及⊙O的半径；
（3）把直线l绕点P旋转，使直线l与⊙O相切，求直线l的解析式.