江西省南昌市九年级上学期期末终结性测试数学试卷
关于x的方程(k+2)x2-kx-2=0必有一个根为( ).
| A.x=1 | B.x=-1 | C.x=2 | D.x=-2 |
抛物线y=-4(x+3)2+1的顶点坐标是( ).
| A.(3,1) | B.(3,-1) | C.(-3,1) | D.(-3,-1) |
将等边△ABC绕自身的内心O,顺时针至少旋转n°,就能与自身重合,则n等于( ).
| A.60 | B.120 | C.180 | D.360 |
如图,两圆圆心相同,大圆的弦AB与小圆相切,AB=2n,则图中阴影部分的面积是( ).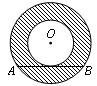
| A.n2π | B.2n2π | C.4n2π | D.8n2π |
如图,在半径为2的扇形OAB中,∠AOB=90°,点C是弧AB上的—个动点(不与A,B重合),OD⊥BC,OE⊥AC,垂足分别为D,E,则DE的长度( )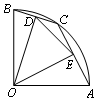
| A.1 | B.2 | C.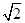 |
D.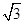 |
如图,它是一个圆锥体的三视图,则这个圆锥的侧面积为( ).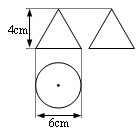
| A.12πcm2 | B.15πcm2 | C.24πcm2 | D.30πcm2 |
盒子里有完全相同的三个小球,球上分别标有数字-2,1,4.随机摸出一个小球,其数字为p(放回),再随机摸出一个小球,其数字记为q,则满足关于x的方程x2+px+q=0有实数根的概率是( ).
A.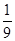 |
B.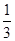 |
C.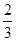 |
D.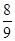 |
反比例函数y=-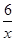 在第二象限的图象上有两点A、B,它们的横坐标分別为-1,-3,直线AB与x轴交于点C,则△AOC的面积为( ).
在第二象限的图象上有两点A、B,它们的横坐标分別为-1,-3,直线AB与x轴交于点C,则△AOC的面积为( ).
A.8 B.10 C.12 D.24
箱子中装有6个只有颜色不同的球,其中1个红球,2个黄球,3个白球.从箱子中随机摸出一个球不是白球的概率是 ,不是黄球的概率是 .
如图,在平面直角坐标系中,直线y=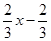 与矩形ABCO的边OC、BC分别交于点E、F,已知OA=3,OC=4,则△CEF的面积是( )
与矩形ABCO的边OC、BC分别交于点E、F,已知OA=3,OC=4,则△CEF的面积是( )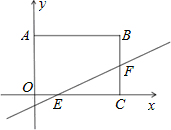
A.6 B.3 C.12 D.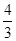
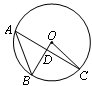
如图,点A、B、C在⊙O上,已知:AC∥OB.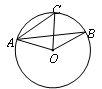
(1)直接写出图中等于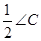 的角;
的角;
(2)如果∠B=25°,求∠AOC的大小.
如图,边长为4cm的等边三角形ABC与⊙O等高(即高与直径相等),⊙O与BC相切于点C,⊙O与AC相交于点E.
求:(1)CE的长;
(2)阴影部分的面积.
有背面一样,正面分别是2、3、4、5的4张扑克牌.两次随机摸一张牌看正面的点数(每一次摸牌后放回).
(1)通过画树状图或列表,列举出所有点数之和的所有可能结果;
(2)求点数之和不超过6的概率P.
如图,己知:反比例函数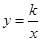 的图象与一次函数y=mx+b的图象交于点A(1,4),点B(-4,n).
的图象与一次函数y=mx+b的图象交于点A(1,4),点B(-4,n).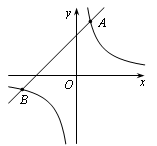
(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积.
某同学报名参加学校运动会,有以下5个项目可供选择:
径赛项目:100m,200m,400m(分别用A1、A2、A3表示);
田赛项目:跳远,跳高(分别用B1、B2表示).
(1)该同学从5个项目中任选一个,恰好是田赛项目的概率为 ;
(2)该同学从5个项目中任选两个,利用树状图或列表列举出所有可能出现的结果,并求恰好是—个田赛项目和一个径赛项目的概率.
【阅读材料】己知,如图1,在面积为S的△ABC中,BC=a,AC=b,AB=c,内切⊙O的半径为r.连接OA、OB、OC,△ABC被划分为三个小三角形.
∵S=S△OBC+S△OAC+S△OAB=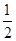 BC·r+
BC·r+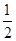 AC·r+
AC·r+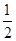 AB·r=
AB·r=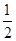 a·r+
a·r+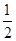 b·r+
b·r+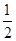 c·r=
c·r=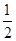 (a+b+c)r
(a+b+c)r
∴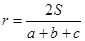
(1)【类比推理】如图2,若面积为S的四边形ABCD存在内切圆(与各边都相切的圆),各边长分别为AB=a,BC=b,CD=c,AD=d,求四边形的内切圆半径r的值;
(2)【理解应用】如图3,在Rt△ABC中,内切圆O的半径为r,⊙O与△ABC分别相切于D、E和F,己知AD=3,BD=2,求r的值.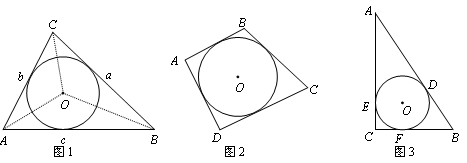
如图,已知:点B(3,3)在双曲线y= (x>0)上,点D在双曲线y=-
(x>0)上,点D在双曲线y=-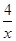 (x<0)上,点A和点C分别在x轴,y轴的正半轴上,且点A,B,C,D构成的四边形为正方形.求:
(x<0)上,点A和点C分别在x轴,y轴的正半轴上,且点A,B,C,D构成的四边形为正方形.求:
(1)k的值;
(2)点A的坐标.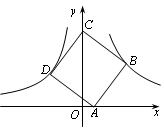
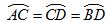 ,M是AB上一动点,CM+DM的最小值是 cm.
,M是AB上一动点,CM+DM的最小值是 cm.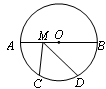
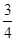 x+b(b为常数,b>0)的图象与x轴、y轴分别相交于点A、B,半径为4的⊙O与x轴正半轴相交于点C,与y轴相交于点D、E,点D在点E上方.
x+b(b为常数,b>0)的图象与x轴、y轴分别相交于点A、B,半径为4的⊙O与x轴正半轴相交于点C,与y轴相交于点D、E,点D在点E上方.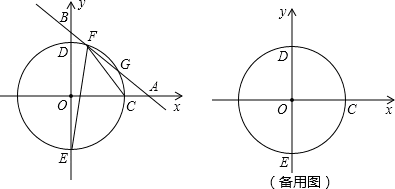
 有两个交点F、G.
有两个交点F、G. 粤公网安备 44130202000953号
粤公网安备 44130202000953号