江苏省盐城东台苏东双语九年级上学期第一次质量检测数学试卷
用配方法解方程x2-2x-1=0时,配方后得的方程为( )
| A.(x+1)2=0 | B.(x-1)2=0 | C.(x+1)2=2 | D.(x-1)2=2 |
一元二次方程x2+x-1="0" 的根的情况为( )
| A.有两个不相等的实数根 | B.有两个相等的实数根 |
| C.只有一个实数根 | D.没有实数根 |
如图,AB是⊙O直径,∠AOC=130°,则∠D=( )
| A.65° | B.25° | C.15° | D.35° |
在数轴上,点A所表示的实数为3,点B所表示的实数为a,⊙ A的半径为2,下列说
法中不正确的是( )
| A.当a<5时,点B在⊙A内 |
| B.当1<a<5时,点B在⊙A内 |
| C.当a<1时,点B在⊙A外 |
| D.当a>5时,点B在⊙A外 |
如图,在平面直角坐标系中,点A、B、C的坐标为(1,4)、(5,4)、(1、 ),则△ABC外接圆的圆心坐标是( )
),则△ABC外接圆的圆心坐标是( )
A.(2,3) B.(3,2) C.(1,3) D.(3,1)
下列四个命题:
①直径是弦;
②经过三个点一定可以作圆;
③三角形的外心到三角形各顶点的距离都相等;
④半径相等的两个半圆是等弧。
其中正确的有( )
| A.4个 | B.3个 | C.2个 | D.1个 |
在平面直角坐标系xOy中,以原点O为圆心的圆过点A(13,0),直线y=kx﹣3k+4与⊙O交于B、C两点,则弦BC的长的最小值为( )
A.22 B.24 C. D.
D.
直角三角形一条直角边和斜边的长分别是一元二次方程x2-16x+60=0的两个实数根,该三角形的面积为 .
如图,C是以AB为直径的⊙O上一点,已知AB=5,BC=3,则圆心O到弦BC的距离是 .
学校组织一次乒乓球赛, 要求每两队之间都要赛一场. 若共赛了15场,则有几个球队参赛?设有 个球队参赛,列出正确的方程___________________.
若正数a是一元二次方程x2﹣5x+m=0的一个根,﹣a是一元二次方程x2+5x﹣m=0的一个根,则a的值是
东台市为打造“绿色城市”,积极投入资金进行河道治污与园林绿化两项工程,已知2013年投资1000万元,预计2015年投资1210万元.若这两年内平均每年投资增长的百分率相同.
(1)求平均每年投资增长的百分率;
(2)按此增长率,计算2016年投资额能否达到1360万?
如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的直线互相垂直,垂足为D,且AC平分∠DAB.
(1)求证:DC为⊙O的切线;
(2)若⊙O的半径为3,AD=4,求AC的长.
每位同学都能感受到日出时美丽的景色.下图是一位同学从照片上剪切下来的画面,“图上”太阳与海平线交于A﹑B两点,他测得“图上”圆的半径为5厘米,AB=8厘米,若从目前太阳所处位置到太阳完全跳出海面的时间为16分钟,求“图上”太阳升起的速度.
在等腰△ABC中,三边分别为a、b、c,其中a=5,若关于 的方程x2+(b+2)x+6-b=0有两个相等的实数根,求△
的方程x2+(b+2)x+6-b=0有两个相等的实数根,求△ 的周长.
的周长.
实践操作:
如图,在 中,∠ABC=90°,利用直尺和圆规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法)
中,∠ABC=90°,利用直尺和圆规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法)
(1)作∠BCA的角平分线,交AB于点O;
(2)以O为圆心,OB为半径作圆.
综合运用:
在你所作的图中,
(1)AC与⊙O的位置关系是 (直接写出答案)
(2)若BC=6,AB=8,求⊙O的半径.
悦达汽车4S店“十一”黄金周销售某种型号汽车,该型号汽车的进价为30万元/辆,若黄金周期间销售量超过5辆时,每多售出1辆,所有售出的汽车进价均降低0.1万元/辆.根据市场调查,黄金周期间销售量不会突破30台.已知该型号汽车的销售价为32万元/辆,悦达汽车4S店计划黄金周期间销售利润25万元,那么需售出多少辆汽车?(注:销售利润=销售价﹣进价)
(1)引入:如图1,直线AB为⊙O的弦,OC⊥OA,交AB于点P,且PC=BC,直线BC是否与⊙O相切,为什么?
(2)引申:记(1)中⊙O的切线为直线 ,在(1)的条件下,如图2,将切线
,在(1)的条件下,如图2,将切线 向下平移,设平移后的直线
向下平移,设平移后的直线 与OB的延长线相交于点
与OB的延长线相交于点 ,与AB的延长线相交于点E,与OP的延长线相交于点
,与AB的延长线相交于点E,与OP的延长线相交于点 .
.
找出图2中与 相等的线段,并说明理由;
相等的线段,并说明理由;
如果 =9cm,
=9cm, =12cm,⊙O的半径为6cm,试求线段
=12cm,⊙O的半径为6cm,试求线段 的长.
的长.
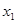 、
、 是一元二次方程
是一元二次方程 的两个根,则
的两个根,则 等于( )
等于( )


 是方程
是方程 的一个根,求
的一个根,求 的值及方程的另一个根.
的值及方程的另一个根.
 上异于C、D的点,线段AB经过点F.
上异于C、D的点,线段AB经过点F. ,在线段AB上是否存在点P,使∠CPE=45°?若存在请求出点P坐标;若不存在,请说明理由.
,在线段AB上是否存在点P,使∠CPE=45°?若存在请求出点P坐标;若不存在,请说明理由. 粤公网安备 44130202000953号
粤公网安备 44130202000953号