初中数学圆幂定理试题

如图，在△ABC中，AB=AC，AE是角平分线，BM平分∠ABC交AE于点M，经过B、M两点的⊙O交BC于点G，交AB于点F，FB恰为⊙O的直径．

（1）判断AE与⊙O的位置关系，并说明理由；
（2）当BC=4，AC=3CE时，求⊙O的半径．

如图，点A、B、C在⊙O上，若∠BAC= 24°，则∠BOC=         °．

如图,AB是半圆的直径,点D是弧AC的中点, ∠ABC=50°，则∠DAB等于（ ）

A．55°

B．60°

C．65°

D．70°

如图，在直角坐标系中，⊙P的圆心P在x轴上，⊙P与x轴交于点E、F，与y轴交于点C、D，且EO=1，CD=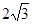，又B、A两点的坐标分别为（0，m）、（5，0）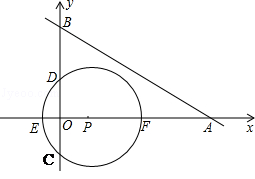

（1）当m=3时，求经过A、B两点的直线解析式；
（2）当B点在y轴上运动时，若直线AB与⊙P保持相交，求m的取值范围．

在圆心角为120°的扇形中，半径为6，则扇形的面积是      ．

直角三角形的两条边长分别为6和8，那么这个三角形的外接圆半径为             

已知圆锥的底面半径为3，侧面积为15，则这个圆锥的高为        ．

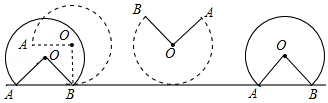
已知一个圆心角为270°扇形工件，未搬动前如图所示，A、B两点触地放置，搬动时，先将扇形以B为圆心，作如图所示的无滑动翻转，再使它紧贴地面滚动，当A、B两点再次触地时停止，半圆的直径为6m，则圆心O所经过的路线长是       m．（结果用含π的式子表示）

如图，∠A是⊙O的圆周角，∠A=50°，则∠BOC的度数为

A．40°

B．50°

C．90°

D．100°

如图，将半径为8的⊙O沿AB折叠，弧AB恰好经过与AB垂直的半径OC的中点D，则折痕AB长为（  ）

A．

B．

C．8

D．10

下列命题：①直径是圆中最长的弦； ②经过三个点一定可以作圆；③三角形的外心到三角形各顶点的距离都相等；④菱形的四个顶点在同一个圆上；其中正确结论的个数有（ ）

A．1个

B．2个

C．3个

D．4个

如图，A．B、C、D是⊙O上的三点，∠BAC=30°，则∠BOC的大小是（   ）

A．60°    B．45°    C．30°    D．15°

如图，在⊙O中，∠ACB=∠BDC=60°，AC=2cm．

（1）求∠BAC的度数；
（2）求⊙O的周长．

如图，的半径为5，AB为的弦，OC⊥AB于点C，若OC=3，则AB的长为________________．

如图，已知正方形ABCD的边长为cm，将正方形ABCD在直线上顺时针连续翻转4次，则点A所经过的路径长为                               【 】

A．4πcm

B．πcm

C．πcm

D．πcm