初中数学圆幂定理试题

在长方形ABCD中AB=16，如图所示裁出一扇形ABE，将扇形围成一个圆锥（AB和AE重合），则此圆锥的底面半径为（）

A．4

B．16

C．4

D．8

已知扇形的圆心角为60°，半径为6，则扇形的面积为（）

A．24π

B．12π

C．6π

D．2π

如图，AB是⊙O的直径，弦CD∥AB．若∠ABD＝65°，则∠ADC＝ °．

如图，在△ABC中，AB=AC，∠A=120°，BC=2，⊙A与BC相切于点D，且交AB，AC于M，N两点，则图中阴影部分的面积是_________ （保留π）．

下列命题中，是真命题的是（）

A．三点确定一个圆

B．长度相等的弧是等弧

C．圆周角等于圆心角的一半

D．正七边形有七条对称轴

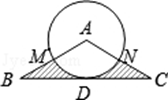
如图，在平面直角坐标系中，⊙P的圆心坐标是（3，a）（a＞3），半径为3，函数y=x的图象被⊙P截得的弦AB的长为，则a的值是（）

A．4

B．

C．

D．

以原点为圆心,为半径的圆分别交、轴的正半轴于A、B两点,点P的坐标为．
（1）如图一，动点Q从点B处出发，沿圆周按顺时针方向匀速运动一周,设经过的时间为秒，当时，直线PQ恰好与⊙O第一次相切，连接OQ．求此时点Q的运动速度（结果保留）；
（2）若点Q按照⑴中的方向和速度继续运动，
①当为何值时，以O、P、Q为顶点的三角形是直角三角形；
②在①的条件下，如果直线PQ与⊙O相交，请求出直线PQ被⊙O所截的弦长．

如图，ABCD的顶点A、B、D在⊙O上，顶点C在⊙O的直径BE上，∠ADC=54°，连接AE，则∠AEB的度数为（ ）

A．36°B．46°C．27°D．63°

已知圆锥的侧面展开图的圆心角为120°，则这个圆锥的侧面积是底面积的 ．

如图，已知⊙O的弦CD垂直于直径AB，点E在CD上，且EC=EB．

（1）求证：△CEB∽△CBD；
（2）若CE=3，CB=5，求DE的长．

如图，AB是⊙O的一条弦，点C是⊙O上一动点，且∠ACB=30°，点E、F分别是AC、BC的中点，直线EF与⊙O交于G、H两点．若⊙O的半径为7，则GE+FH的最大值为 ．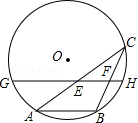

如图，△ABC内接于⊙O，CD是⊙O的直径，∠A =35°，则∠BCD的度数是（）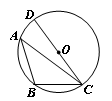

A．55°

B．65°

C．70°

D．75°

如图，AB是⊙O的直径，BD，CD分别是过⊙O上点B，C的切线，且∠BDC＝110°．连接AC，则∠A的度数是______°．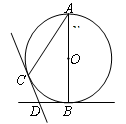

已知⊙O的半径是5，直线l是⊙O的切线，P是l上的任一点，那么下列结论正确的是

A．0＜OP＜5

B．OP＝5

C．OP＞5

D．OP≥5

设同一个圆的内接正六边形、正八边形、正十二边形的边心距分别为r₆，r₈，r₁₂，则r₆，r₈，r₁₂的大小关系为（）

A．r6＞r8＞r12

B．r6＜r8＜r12

C．r8＞r6＞r12

D．不能确定