初中数学一次函数的最值解答题

某果品批发公司以16元/千克购进一批樱桃．由往年市场销售情况的统计分析可知：当销售价定为25 元/千克时，每天可售出1 000 千克；若销售价定为20元/千克时，每天可售出2000千克．假设每天的销售量y（千克）与销售价x（元/千克）之间满足一次函数．
（1）试求y与x之间的函数关系式；
（2）在商品无积压且不考虑其他因素的条件下，销售价格定为多少时，才能使每天的销售毛利润W（元）最大？最大利润是多少？

学习“一次函数”时，我们从“数”和“形”两方面研究一次函数的性质，并积累了一些经验和方法，尝试用你积累的经验和方法解决下面问题．
（1）在平面直角坐标系中，画出函数y=|x|的图象：
①列表：完成表格

x	…	﹣3	﹣2	﹣1	0	1	2	3	…
y	…

 
②画出y=|x|的图象；
（2）结合所画函数图象，写出y=|x|两条不同类型的性质；
（3）直接写出函数y=|x﹣2|图象是由函数y=|x|图象怎样平移得到？

已知一次函数y＝▓▓的图像过点A（0,3），B（2,4），C（m，0）题目中的阴影部分是一段因墨水污染而无法辨认的文字．
（1）根据已有的信息你能求出一次函数的表达式吗？若能，写出解题过程；不能，说明理由
（2）小明说“不用求表达式也能画出函数的图像”你认为对吗？为什么？
（3）根据表达式画出函数图像
（4）过点B能不能画一条直线将△ABO（O为坐标原点）分成面积比为1:2两部分？若能可以画几条？并写出此直线对应的函数表达式

在计算3+5+7+9+11+13的值时，小明直接计算出结果为48，爱动脑筋的小红，发现这6个数据的特点后，用的方法来计算，也得出同样的结果．
请用上面小红的发现解答下面问题：
某公司对外出租一商铺，符合条件的两商户A、B分别拟定上缴利润方案如下：
A：每年结算一次上缴房租，第一年上缴1．5万元，以后每年比前一年增加1万元；
B：每半年结算一次上缴房租，第一个半年上缴0．3万元，以后每半年比前半年增加0．3万元；
（1）如果承租期限3年，则A商户上缴房租的总金额为           万元，B商户上缴房租的总金额为________万元；
（2）如果承租期限为n年，分别求A、B两商户上缴房租的总金额；（用含n的代数式表示）
（3）如果承租期限n=20时，那么哪个商户上缴房租的总金额比较多？

先阅读短文，然后回答短文后面所给出的问题：
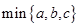对于三个数a、b、c的平均数，最小的数都可以给出符号来表示，我们规定 表示这三个数的平均数，表示这三个数中的最小的数，表示这三个数中最大的数．例如：，，；，．
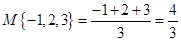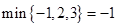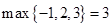（1）请填空：      ；若，则      ；
（2）若，求的取值范围；
（3）若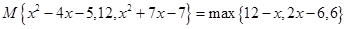，求的值．

已知到直线l的距离等于a的所有点的集合是与直线l平行且距离为a的两条直线l_1、l₂（图①）．

（1）在图②的平面直角坐标系中，画出到直线的距离为1的所有点的集合的图形，并写出该图形与y轴交点的坐标；
（2）试探讨在以坐标原点O为圆心，r为半径的圆上，到直线的距离为1的点的个数与r的关系；
（3）如图③，若以坐标原点O为圆心，2为半径的圆上有两个点到直线的距离为1，则 b的取值范围为____________________________________________．

如图①，已知直线y=3x+3与x轴交于点A，与y轴交于点D，与直线y=交于点E，
过点D作DC∥x轴，交直线y=于点C．过点C作CB∥AD交x轴于点B．
（1）点C的坐标是      ；
（2）以线段AD的中点M为圆心作⊙M，当⊙M与直线CE相切时，求⊙M的半径；
（3）如图②，点P从点O出发，沿线段OC向终点C运动，点Q从点C出发，沿线段CD向终点D运动．若P、Q两点同时出发，速度均为1单位长度/s，时间为ts，当点Q到达终点时，P、Q两点均停止运动．在点P、Q的运动过程中，将线段PQ绕点P沿顺时针方向旋转90°后，设点Q的对应点为R．当点R落在四边形ABCD一边所在的直线上时，直接写出t的值．

某公司生产一种环保产品，需要添加一种新型原料，若每件产品的利润与新型原料价格成一次函数关系，且每件产品的利润y（元）与新型原料的价格x（元/千克）的函数图象如图：

（1）当新型原料的价格为600元/千克时，每件产品的利润是多少？
（2）新型原料是一种稀少材料，为了珍惜资源，政府部门规定：新型原料每天使用量m（千克）与价格x（元/千克）的函数关系为x ="10m" +500，且m千克新型原料可生产10m件产品．那么生产300件这种产品，一共可得利润是多少？
（3）受生产能力的限制，该公司每天生产这种产品不超过450件，那么在（2）的条件下，该公司每天应生产多少件产品才能获得最大利润？最大利润是多少？

在平面直角坐标系中，△ABC的边AB在x轴上，且OA＞OB，以AB为直径的圆与y轴正半轴交于点C，A、B两点的横坐标x_A、x_B是关于x的方程x²＋3x－4=0的两个根．

（1）求点C的坐标；
（2）若∠ACB的平分线所在的直线l交x轴于点D，求直线l对应的一次函数关系式；
（3）过点D任作一直线l′分别交射线CA、CB（点C除外）于点M、N，则＋的值是否为定值？若是，求出定值；若不是，请说明理由．

如图，在平面直角坐标系中，O为坐标原点．A．B两点的坐标分别为A（m，0）、B（0，n），且，点P从A出发，以每秒1个单位的速度沿射线AO匀速运动，设点P运动时间为t秒．
（1）求m、n的值与OA、OB的长；
（2）连接PB，若△POB的面积不大于3且不等于0，则t的取值范围是          （请直接写出答案）．
（3）过P作直线AB的垂线，垂足为D，直线PD与y轴交于点E，在点P运动的过程中，是否存在这样的点P，使△EOP≌△AOB？若存在，请求出t的值；若不存在，请说明理由．
        

为了能有效地使用电力资源，跃进花园小区实行居民峰谷用电，居民家庭在峰时段（上午8：00—晚上21：00）用电的电价为0．55元/度，谷时段（晚上21：00—次日晨8：00）用电的电价为0．35元/度．
（1）若朱老师家某月用电100度，其中峰时段用电度，这个月应缴纳电费      度；当朱老师家峰时段用电60度时，求应缴纳电费．
（2）朱老师生活节俭，每天早晨5：30起身后立即用额定功率1500瓦的电水壶烧水，10分钟能烧开一壶水。问朱老师家一年内用电水壶烧水共耗电多少度？能节省电费多少元？（一年按实际烧水360天计算，1度=1千瓦．时）

学校需要到印刷厂印刷x份材料，甲印刷厂提出：每份材料收0.2元印刷费，另收500元制版费；乙印刷厂提出：每份材料收0.4元印刷费，不收制版费．
（1）两印刷厂的收费各是多少元？（用含x的代数式表示）
（2）学校要印刷2400份材料，若不考虑其他因素，选择哪家印刷厂比较合算？试说明理由．

某空调器销售商，今年四月份销出空调（a﹣1）台，五月份销售空调比四月份的2倍少1台，六月份销售空调比前两个月的总和的4倍还多5台．
（1）用代数式表示该销售商今年第二季度共销售空调多少台？
（2）若a=220，求第二季度销售的空调总数．

如图，在△ABC中，∠BAC=90°，AB=AC=6，D为BC的中点．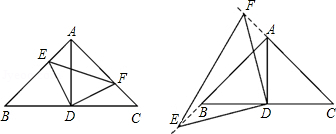

（1）若E、F分别是AB、AC上的点，且AE=CF，求证：△AED≌△CFD；
（2）当点F、E分别从C、A两点同时出发，以每秒1个单位长度的速度沿CA、AB运动，到点A、B时停止；设△DEF的面积为y，F点运动的时间为x，求y与x的函数关系式；
（3）在（2）的条件下，点F、E分别沿CA、AB的延长线继续运动，求此时y与x的函数关系式．

如图1，已知：抛物线y=x²+bx+c与x轴交于A，B两点，与y轴交于点C，经过B，C两点的直线是y=x-2，连结AC．

（1）求出抛物线的函数关系式；
（2）若△ABC内部能否截出面积最大的矩形DEFC（顶点D、E、F、G在△ABC各边上）？若能，求出在AB边上的矩形顶点的坐标；若不能，请说明理由．
（3）点P（t，0）是x轴上一动点，P、Q两点关于直线BC成轴对称，PQ交BC于点M，作QH⊥x轴于点H．连结OQ，是否存在t的值，使△OQH与△APM相似？若存在，求出t的值；若不存在，说明理由．