初中数学一次函数的最值解答题

如图，在平面直角坐标系内，点A的坐标为（0，12），经过原点的直线l，与经过点A的直线1₂相交于点B，点B的坐标为（9，3）．

（1）求直线l₁，l₂的表达式；
（2）点C为直线l₁上一动点，作CD∥y轴交直线l₂于点D，若CD=8，求点C的坐标．

如图，直线l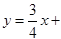：3交x、y轴分别为A、B两点，C点与A点关于y轴对称。动点P、Q分别在线段AC、AB上（点P不与点A、C重合），满足∠BPQ=∠BAO．

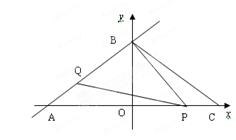
（1）点A坐标是     ，点B的坐标         ，BC=         ．
（2）当点P在什么位置时，△APQ≌△CBP，说明理由。
（3）当△PQB为等腰三角形时，求点P的坐标。

甲、乙两车从A地驶向B地，甲车比乙车早行驶2h，并且在途中休息了0．5h，休息前后速度相同，如图是甲乙两车行驶的距离y（km）与时间x（h）的函数图象．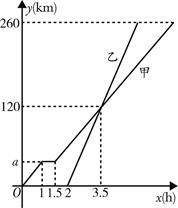

（1）求出图中a的值；
（2）求出甲车行驶路程y（km）与时间x（h）的函数表达式，并写出相应的x的取值范围；
（3）当甲车行驶多长时间时，两车恰好相距20km．

一辆快车从甲地开往乙地，一辆慢车从乙地开往甲地，两车同时出发，设慢车离乙地的距离为（km），快车离乙地的距离为（km），慢车行驶时间为x（h），两车之间的距离为S（km），，与x的函数关系图象如图（1）所示，S与x的函数关系图象如图（2）所示：

（1）图中的a=      ，b=      ；
（2）求S关于x的函数关系式；
（3）甲、乙两地间依次有E、F两个加油站，相距200km，若慢车进入E站加油时，快车恰好进入F站加油．求E加油站到甲地的距离．

某商场计划购进A，B两种新型节能台灯共100盏，这两种台灯的进价、售价如表所示：

（1）设商场购进A型节能台灯为x盏，销售完这批台灯时可获利为y元，求y关于x的函数解析式；
（2）若商场规定B型台灯的进货数量不超过A型台灯数量的3倍，应怎样进货才能使商场在销售完这批台灯时获利最多？此时利润为多少元？

已知直线经过点A（5，0），B（1，4）．
（1）求直线AB的解析式；
（2）若直线与直线AB相交于点C，求点C的坐标；
（3）根据图象，写出关于x的不等式的解集．

某物流公司的快递车和货车同时从甲地出发，以各自的速度匀速向乙地行驶，快递车到达乙地后缷完物品再另装货物共用45分钟，立即按原路以另一速度匀速返回，直至与货车相遇．已知货车的速度为60千米/时，两车之间的距离y（千米）与货车行驶时间x（小时）之间的函数图象如图所示，现有以下4个结论：

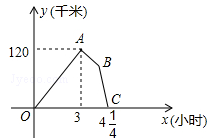
①快递车从甲地到乙地的速度为100千米/时；
②甲、乙两地之间的距离为120千米；
③图中点B的坐标为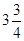（，75）；
④快递车从乙地返回时的速度为90千米/时，以上4个结论正确的是      ．

如图，直线y=x＋3的图象与x轴、y轴交于A、B两点．直线l经过原点，与线段AB交于点C，把△AOB的面积分为2：1两部分．求直线l的解析式．

已知一次函数图象经过A（－2，－3），B（1，3）两点．
（1）求这个一次函数解析式．
（2）试判断点P（－1，1）是否在这个一次函数的图象上？

如图，已知直线AB分别交轴、轴于点A（－2，0），B（0，2），点C是直线AB上一点，且∠ACO=30°，求AC的长及点C的坐标．

（本题8分）如图，在平面直角坐标系中，O是坐标原点，点A坐标为（2，0），点B坐标为（0，b）（b＞0），点P是直线AB上位于第二象限内的一个动点，过点P作PC垂直于x轴于点C，记点P关于y轴的对称点为Q，设点P的横坐标为a．

（1）当b=3时：①求直线AB相应的函数表达式；②当S_△QOA=4时，求点P的坐标；
（2）是否同时存在a、b，使得△QAC是等腰直角三角形？若存在，求出所有满足条件的a、b的值；若不存在，请说明理由．

（本题10分）如图，在平面直角坐标系中，直线＋2与x轴、y轴分别交于A、B两点，以AB为边在第二象限内作正方形ABCD．

（1）求点A、B的坐标，并求边AB的长；
（2）求点D和点C的坐标；
（3）你能否在x轴上找一点M，使△MDB的周长最小?如果能，请求出M点的坐标；如果不能，说明理由．

（本题8分）为了发展旅游经济，我市某景区采用灵活的售票方法吸引游客．门票定价为50元/人，非节假日打a折售票，节假日按团队人数分段定价售票，即m人以下（含m人）的团队按原价售票；超过m人的团队，其中m人仍按原价售票，超过m人部分的游客打b折售票．设某旅游团人数为x人，非节假日购票金额为y₁（元），节假日购票金额为y₂（元）．y₁、y₂与x之间的函数关系如图所示．

（1）观察图象可知：a＝_______；b＝_______；m＝_______．
（2）直接写出y₁、y₂与x之间的函数关系式．
（3）某旅行社导游王娜于5月1日带A团，5月20日（非节假日）带B团都到该景区旅游，共付门票款1900元，A、B两个团队合计50人，A、B两个团队各有多少人？

（本题6分）已知点P（m，n）在第一象限，并且在一次函数y＝2x－1的图像上，求实数m的取值范围．

（本题8分）已知一次函数y=kx+b的图象经过点A（—1，—5），且与正比例函数的图象相交于点B（2，a）．

（1）求a的值；
（2）求一次函数y=kx+b的表达式；
（3）在同一坐标系中，画出这两个函数的图象，并求这两条直线与y轴围成的三角形的面积．