初中数学一次函数的最值解答题

如图，已知直线y=x+1与y轴交于点A，一次函数y=kx+b的图象经过点B（0，-1），并且与x轴以及直线y=x+1分别交于点C、D．

（1）求直线BD的函数表达式；
（2）求四边形AOCD的面积；
（3）在y轴上是否存在这样的点P，使得以P、B、D为顶点的三角形是等腰三角形．如果存在，求出点P的坐标；如果不存在，说明理由．

小轿车从甲地出发驶往乙地，同时货车从相距乙地60km的入口处驶往甲地（两车均在甲、乙两地之间的公路上匀速行驶），如图是它们离甲地的路程y（km）与货车行驶时间x（h）之间的函数的部分图象．

（1）求货车离甲地的路程y（km）与它的行驶时间x（h）的函数关系式；
（2）哪一辆车先到达目的地？说明理由．

已知关于x的一次函数y＝mx＋2的图像经过点（－2，6）．
（1）求m的值；
（2）画出此函数的图像；

某市政府为了增强城镇居民抵御大病风险的能力，积极完善城镇居民医疗保险制度，纳入医疗保险的居民的大病住院医疗费用的报销比例标准如下表：

医疗费用范围	报销比例标准
不超过8000元	不予报销
超过8000元且不超过30000元的部分	50%
超过30000元且不超过50000元的部分	60%
超过50000元的部分	70%

 
设享受医保的某居民一年的大病住院医疗费用为x元，按上述标准报销的金额为y元．
（1）直接写出x≤50000时，y关于x的函数关系式，并注明自变量x的取值范围；
（2）若某居民大病住院医疗费用按标准报销了20000元，问他住院医疗费用是多少元？

某长途汽车客运公司规定旅客可免费携带一定质量的行李，当行李的质量超过规定时，需要购买行李票．已知行李费y（元）是行李质量x（kg）之间的函数表达式为y=kx+b．这个函数的图像如图所示：

（1）求k和b的值；
（2）求旅客最多可免费携带行李的质量；
（3）求行李费为4～15元时，旅客携带行李的质量为多少？

已知y与x﹣3成正比例，当x=4时，y=3
（1）求y与x的函数式；
（2）当x=2时，求y的值．

画出函数y＝－3x＋2的图像
（1）试判断点P（2，-5）是否在此函数的图像上，并说明理由．
（2）求出此直线与坐标轴交点的坐标以及此直线与坐标轴所围成的三角形面积．

如图，直线y=k（x-2）+k-1与x轴、y轴分别交于B、C两点，且．

（1）求B点坐标和k值；
（2）若点A（x，y）是直线y=k（x-2）+k-1（k>0）上在第一象限内的一个动点，
①当点A在运动过程中，试写出△AOB的面积S与x的函数关系式；（不要求写出自变量的取值范围）
②当A点运动到什么位置时，△AOB的面积为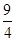，并说明理由；
③在②成立的情况下，x轴上是否存在一点P，使△AOP是等腰三角形？若存在，请直接写出满足条件的所有P点坐标；若不存在，请说明理由．

某业主贷款2．2万元购进一台机器，生产某种产品。已知产品的成本是每个5元，售价是每个8元，应付的税款和其他费用是售价的10％。若每个月能生产、销售2000个产品，问至少几个月后能赚回这台机器的贷款？

已知：如图，在平面直角坐标系xoy中，一次函数y=x+3的图象与x轴和y轴交于A、B两点，将△AOB绕点O顺时针旋转90°后得到△A′OB′．

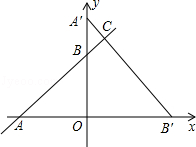
（1）求直线A′B′的解析式；
（2）若直线A′B′与直线AB相交于点C，求S_△A´BC：S_△ABO的值．

“五•一”假期，某火车客运站旅客流量不断增大，旅客往往需要长时间排队等候检票．经调查发现，在车站开始检票时，有640人排队检票．检票开始后，仍有旅客继续前来排队检票进站．设旅客按固定的速度增加，检票口检票的速度也是固定的．检票时，每分钟候车室新增排队检票进站16人，每分钟每个检票口检票14人．已知检票的前a分钟只开放了两个检票口．某一天候车室排队等候检票的人数y（人）与检票时间x（分钟）的关系如图所示．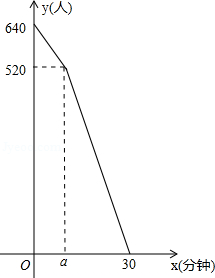

（1）求a的值．
（2）求检票到第20分钟时，候车室排队等候检票的旅客人数．
（3）若要在开始检票后15分钟内让所有排队的旅客都能检票进站，以便后来到站的旅客随到随检，问检票一开始至少需要同时开放几个检票口？

已知一次函数y=kx+b的图象经过点（﹣1，﹣5），且与正比例函数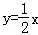的图象相交于点（2，m）．
求：（1）m的值；     
（2）一次函数y=kx+b的解析式；
（3）这两个函数图象与x轴所围成的三角形面积．

“五•一”假期，某火车客运站旅客流量不断增大，旅客往往需要长时间排队等候检票．经调查发现，在车站开始检票时，有640人排队检票．检票开始后，仍有旅客继续前来排队检票进站．设旅客按固定的速度增加，检票口检票的速度也是固定的．检票时，每分钟候车室新增排队检票进站16人，每分钟每个检票口检票14人．已知检票的前a分钟只开放了两个检票口．某一天候车室排队等候检票的人数y（人）与检票时间x（分钟）的关系如图所示．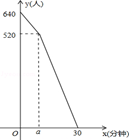

（1）求a的值．
（2）求检票到第20分钟时，候车室排队等候检票的旅客人数．
（3）若要在开始检票后15分钟内让所有排队的旅客都能检票进站，以便后来到站的旅客随到随检，问检票一开始至少需要同时开放几个检票口？

国庆长假，小明从老家乘车去上海．一路上，小明记下了如下数据（注：“上海90km”表示离上海的距离为90km）：

观察时间	10：30（t=0）	10：36（t=6）	10：30（t=18）
路牌内容	上海90Km	上海80Km	上海60Km

 
假设汽车离上海的距离s（km）是行驶时间t（min）的一次函数，求s关于t的函数关系式．

如图，A（0，1），M（3，2），N（4，4） ， 动点P从点A出发，沿y轴以每秒1个单位长的速度向上移动，且过点P的直线l：y＝－x+b也随之移动，设移动时间为 t 秒．（直线y = kx+b平移时k不变）

（1）当t＝3时，求 l 的解析式；
（2）若点M，N位于l 的异侧，确定 t 的取值范围．