初中数学一次函数的最值解答题

已知一次函数y=kx+b的图象经过点(-1, -5),且与正比例函数y= x的图象相交于点(2,a),求
(1)a的值       
(2)k,b的值
(3)这两个函数图象与x轴所围成的三角形面积.

甲乙两人同时登山，甲、乙两人距地面的高度（米）与登山时间之间的函数图象如图所示，根据图象所提供的信息解答下列问题：

（1）甲登山的速度是每分钟    米，乙在地提速时距地面的高度为  ____米；
（2）若乙提速后，乙的速度是甲登山速度的3倍，请分别求出甲、乙二人登山全过程中，登山时距地面的高度（米）与登山时间之间的函数关系式；
（3）登山多长时间时，乙追上了甲？

如图，已知 ， 是一次函数 的图像和反比例函数 的
图像的两个交点

(1)求反比例函数和一次函数的解析式；
(2)求直线 与 轴的交点 的坐标及 的面积．

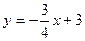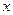如图，已知一次函数的图象与轴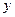，轴分别相交于A，B两点，点C在AB上以每秒1个单位的速度从点B向点A运动，同时点D在线段AO上以同样的速度从点A向点O运动，运动时间用（单位：秒）表示．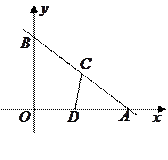

（1）求AB的长；
（2）当为何值时，△ACD与△ABO相似？并直接写出此时点C的坐标．

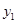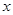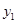一辆客车从甲地开往乙地，一辆出租车从乙地开往甲地，两车同时出发，设客车离甲地的距离为（km），出租车离甲地的距离为（km），客车行驶时间为（h），，与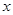的函数关系图象如图所示：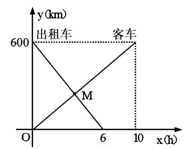

（1）根据图象，求出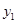，关于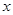的函数关系式。
（2）出发多长时间后两车相遇？此时出租车行驶了多少千米？

如图，一次函数的图象与反比例函数的图象交于点P，点P在第一象限．PA⊥x轴于点A，PB⊥y轴于点B．一次函数的图象分别交轴、轴于点C、D，且S△PBD=4，．

（1）求点D的坐标；
（2）求k、m的值

点P(1，)在反比例函数的图象上，点P关于轴的对称点在一次函数的图象上，求此反比例函数的解析式

玉树地震发生后，根据救灾指挥中心的信息，甲、乙两个重灾区急需一种大型挖掘机，甲地需要27台，乙地需要25台；A、B两省获知情况后慷慨相助，分别捐赠该型号挖掘机28台和24台，并将其全部调运往灾区，如果从A省调运一台挖掘机到甲地耗资0.4万元，到乙地耗资0.3万元；从B省调运一台挖掘机到甲地耗资0.5万元，到乙地耗资0.2万元；设从A调往甲地x台挖掘机，A、B两省将捐赠的挖掘机全部调往灾区共耗资y万元：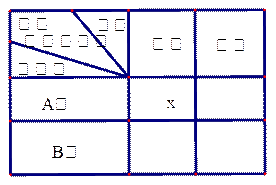

(1)请完成表格的填空：
(2)求出y与x之间的函数关系式，并直接写出自变量x的取值范围
(3)画出这个函数的图象，结合图象说明若要使总耗资不超过16.2万元，有哪几种调运方案？哪种调运方案的总耗资最少？

(1)点(1，3)沿X轴的正方向平移4个单位得到的点的坐标是_________
(2)直线y=3x沿x轴的正方向平移4个单位得到的直线解析式为____________
(3)若直线l与(2)中所得的直线关于直线x=2对称，试求直线l的解析式．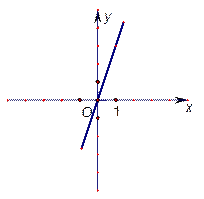

如图1：直线y= kx+4k（k≠0）交x轴于点A，交y轴于点C，点M(2，m)为直线AC上一点，过点M的直线BD交x轴于点B，交y轴于点D．

(1)求的值（用含有k的式子表示．）；
(2)若SBOM =3SDOM，且k为方程(k+7)(k+5)-(k+6)(k+5=的根，求直线BD的解析式．
(3)如图2，在(2)的条件下，P为线段OD之间的动点（点P不与点O和点D重合），OE
上AP于E，，DF上AP于F，下列两个结论：①值不变；②值不变，请你判断其中哪一个结论是正确的，并说明理由并求出其值，

已知y-2与x成正比例，当x=3时，y=1，求y与x的函数表达式

为了预防流感，学校对教室进行“药熏消毒”。已知药物燃烧阶段，室内每立方米空气中的含药量y（mg）与燃烧时间x（分钟）成正比，燃烧后，y与x成反比（如图所示），现测得药物10分钟燃烧完，此时教室内每立方米空气含药量为16mg。根据以上信息解答下列问题： 

（1）求药物燃烧时以及药物燃烧后y与x的函数关系式；
（2）当每立方米空气中含药量低于4mg时对人体无害，那么从消毒开始经多长时间后学生才能进教室？   
（3）当每立方米空气中药物含量不低于8mg且持续时间不低于25分钟时消毒才有效，那么这次消毒效果如何？

如图，一次函数y=kx+b与反比例函数.（mk≠0）图像交于A（—4，2）B(2，n)两点。

（1）求一次函数和反比例函数的表达式；
（2）求△ABO的面积；
（3）当x取非零的实数时，试比较一次函数值与反比例函数值的大小

为了扶持大学生自主创业，市政府提供了80万元无息贷款，用于某大学生开办公司生产并销售自主研发的一种电子产品，并约定用该公司经营的利润逐步偿还无息贷款．已知该产品的生产成本为每件40元，员工每人每月的工资为2500元，公司每月需支付其它费用15万元．
该产品每月销售量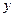（万件）与销售单价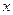（元）之间的函数关系如图所示．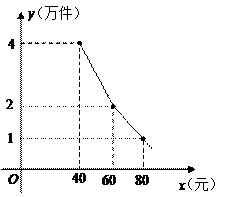

（1）求月销售量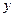（万件）与销售单价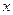（元）之间的函数关系式；
（2）当销售单价定为50元时，为保证公司月利润达到5万元
（利润＝销售额－生产成本－员工工资－其它费用），该公司可安排员工多少人？
（3）若该公司有80名员工，则该公司最早可在几个月后还清无息贷款？

小明平时喜欢玩“QQ农场”游戏，本学期初二年级数学备课组组织了几次数学反馈性测试，小明的数学成绩如下表：

月份x（月）	9	10	11	12	…
成绩y	90	80	70	60	…

（1）以月份为x轴，成绩为y轴，根据上表提供的数据在下列直角坐标系中描点；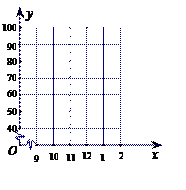

（2）观察①中所描点的位置关系，照这样的发展趋势，猜想y与x之间的函数关系，并求出所猜想的函数表达式；
（3）若小明继续沉溺于“QQ农场”游戏，照这样的发展趋势，请你估计元月份的期末考试中小明的数学成绩，并用一句话对小明提出一些建议．