初中数学一次函数的最值解答题

某种洗衣机在洗涤衣服时，经历了进水、清洗、排水、脱水四个连续的过程，其中进水、清洗、排水时洗衣机中的水量(升)与时间(分钟)之间的关系如折线图所示：

根据图象解答下列问题：
（1）洗衣机的进水时间是多少分钟？清洗时洗衣机中的水量是多少升？
（2）已知洗衣机的排水速度为每分钟19升．
①求排水时与之间的关系式；
②如果排水时间为2分钟，求排水结束时洗衣机中剩下的水量．

据某气象中心观察和预测：发生于地的沙尘暴一直向正南方向移动，其移动速度（km/h）与时间（h）的函数图象如图所示．过线段上一点作横轴的垂线，梯形在直线左侧部分的面积即为h内沙尘暴所经过的路程(km)．

（1）当时，求的值；
（2）将s随变化的规律用数学关系式表示出来；
（3）若城位于地正南方向，且距地650km，试判断这场沙尘暴是否会侵袭到城．如果会，在沙尘暴发生后多长时间它将侵袭到城？如果不会，请说明理由．

周华早起锻炼，往返于家与体育场之间，离家的距离y(米)与时间x(分)的关系如图所示．回答下列问题：

(1)填空：周华从体育场返回行走的行走速度时___________米/分；
(2)刘明与周华同时出发，按相同的路线前往体育场，刘明离周华家的距离y(米)与时间x(分)的关系式为y＝kx＋400，当周华回到家时，刘明刚好到达体育场．
①直接在图中画出刘明离周华家的距离y(米)与时间x(分)的函数图象；
②填空：周华与刘明在途中共相遇___________次；
③求周华出发后经过多少分钟与刘明最后一次相遇．

如图，⊙的半径为，正方形顶点坐标为，顶点在⊙上运动．
(1)当点运动到与点、在同一条直线上时,试证明直线与⊙相切；
(2)当直线与⊙相切时，求所在直线对应的函数关系式；
(3)设点的横坐标为，正方形的面积为，求与之间的函数关系式，并求出的最大值与最小值．

一列快车从甲地驶往乙地，一列慢车从乙地驶往甲地，两车同时出发，设慢车行驶的时间为x（h），两车之间的距离为y（km），图中的折线表示y与x之间的函数关系．根据图象进行以下探究：
信息读取：
（1）甲、乙两地之间的距离为km；
（2）请解释图中点B的实际意义；
图象理解：
（3）求慢车和快车的速度；
（4）求线段BC所表示的y与x之间的函数关系式，并写出自变量x的取值范围；
问题解决：
（5）若第二列快车也从甲地出发驶往乙地，速度与第一列快车相同．在第一列快车与慢车相遇30分钟后，第二列快车与慢车相遇．求第二列快车比第一列快车晚出发多少小时？

如图，在平面直角坐标系中，O为坐标原点为，B（5,0），M为等腰梯形OBCD底边OB上一点，OD＝BC＝2，∠DMC＝∠DOB＝60°．

（1）求直线CB的解析式；
（2）求点M的坐标；
（3）∠DMC绕点M顺时针旋转α　（30°＜α＜60°）后，得到∠D₁MC₁（点D₁，C₁依次与点D，C对应），射线MD₁交直线DC于点E，射线MC1交直线CB于点F　，设DE＝m，BF＝n .求m与　n的函数关系式．

某中学的高中部在校区，初中部在校区，学校学生会计划在3月12日植树节当天安排部分学生到郊区公园参加植树活动.已知校区的每位高中学生往返车费是6元，每人每天可栽植5棵树；校区的每位初中学生往返车费是10元，每人每天可栽植3棵树.要求初高中均有学生参加，且参加活动的初中学生比参加活动的高中学生多4人，本次活动的往返车费总和不得超过210元.要使本次活动植树最多，初高中各有多少学生参加？最多植树多少棵？

某蔬菜加工厂承担出口蔬菜加工任务，有一批蔬菜产品需要装入某一规格的纸箱．供应这种纸箱有两种方案可供选择：
方案一：从纸箱厂定制购买，每个纸箱价格为4元；
方案二：由蔬菜加工厂租赁机器自己加工制作这种纸箱，机器租赁费按生产纸箱数收取．工厂需要一次性投入机器安装等费用16000元，每加工一个纸箱还需成本费2.4元．
（1）若需要这种规格的纸箱个，请分别写出从纸箱厂购买纸箱的费用（元）和蔬菜加工厂自己加工制作纸箱的费用（元）关于（个）的函数关系式；
（2）假设你是决策者，你认为应该选择哪种方案？并说明理由．

如图，在直角坐标系中△ABC的A、B、C三点坐标为A(7，1)、B(8，2)、C(9，0)．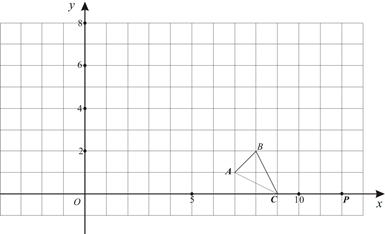

(1) 请在图中画出△ABC的一个以点P (12，0)为位似中心，相似比为3的位似图形(要求与△ABC同在P点一侧);
(2)求线段BC的对应线段所在直线的解析式．

某冰箱厂为响应国家“家电下乡”号召，计划生产、两种型号的冰箱100台．经预算，两种冰箱全部售出后，可获得利润不低于 4.75万元，不高于4.8万元，两种型号的冰箱生产成本和售价如下表：

型号	A型	B型
成本（元/台）	2200	2600
售价（元/台）	2800	3000

（1）冰箱厂有哪几种生产方案？
（2）该冰箱厂按哪种方案生产，才能使投入成本最少？“家电下乡”后农民买家电（冰箱、彩电、洗衣机）可享受13%的政府补贴，那么在这种方案下政府需补贴给农民多少元？
（3）若按（2）中的方案生产，冰箱厂计划将获得的全部利润购买三种物品：体育器材、实验设备、办公用品支援某希望小学．其中体育器材至多买4套，体育器材每套6000元，实验设备每套3000元，办公用品每套1800元，把钱全部用尽且三种物品都购买的情况下，请你直接写出实验设备的买法共有多少种．

甲、乙两车同时从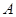地出发，以各自的速度匀速向地行驶．甲车先到达地，停留1小时后按原路以另一速度匀速返回，直到两车相遇．乙车的速度为每小时60千米．下图是两车之间的距离（千米）与乙车行驶时间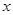（小时）之间的函数图象．
（1）请将图中的（  ）内填上正确的值，并直接写出甲车从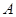到的行驶速度；
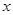（2）求从甲车返回到与乙车相遇过程中与之间的函数关系式，并写出自变量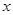的取值范围．
（3）求出甲车返回时行驶速度及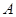、两地的距离．

在“五一黄金周”期间，小明和他的父母坐游船从甲地到乙地观光，在售票大厅看到表（一）， 爸爸对小明说：“我来考考你，你能知道里程与票价之间有何关系吗？”小明点了点头说：“里程与票价是一次函数关系，具体是……”．

在游船上，他注意到表（二），思考一下，对爸爸说：“若游船在静水中的速度不变，那么我还能算出它的速度和水流速度．”爸爸说：“你真聪明！”亲爱的同学，你知道小明是如何求出的吗？请你和小明一起求出：

（1）票价（元）与里程（千米）的函数关系式；
（2）游船在静水中的速度和水流速度．

暑假期间，小明和父母一起开车到距家200千米的景点旅游.出发前，汽车油箱内储油45升；当行驶150千米时，发现油箱剩余油量为30升.
(1)已知油箱内余油量y(升)是行驶路程x(千米)的一次函数，求y与x的函数关系式；
(2)当油箱中余油量少于3升时，汽车将自动报警.如果往返途中不加油，他们能否在汽车报警前回到家?请说明理由.

某地区一种商品的需求量 $y_1$（万件）、供应量 $y_2$（万件）与价格（元／件）分别近似满足下列函数关系式： $y_1=-x+60$， $y_2=2x-36$．需求量为0时，即停止供应．当 $y_1=y_2$时，该商品的价格称为稳定价格，需求量称为稳定需求量．

（1）求该商品的稳定价格与稳定需求量；
（2）价格在什么范围，该商品的需求量低于供应量？
（3）当需求量高于供应量时，政府常通过对供应方提供价格补贴来提高供货价格，以提高供应量．现若要使稳定需求量增加4万件，政府应对每件商品提供多少元补贴，才能使供应量等于需求量？

在平面直角坐标系中,直线经过点A（,4）,且与轴相交于点C.点B在轴上,O为为坐标原点,且.记的面积为S.
（1）求m的取值范围;
（2）求S关于m的函数关系式;
（3）设点B在轴的正半轴上,当S取得最大值时,将沿AC折叠得到,求点的坐标.